
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
【答案】(1)原计划每天生产零件2400个,规定的天数是10天;(2)原计划安排的工人人数为480人.
【解析】试题分析:(1)设原计划每天生产零件x个,根据相等关系“原计划生产24000个零件所用时间=实际生产(24000+300)个零件所用的时间”可列方程![]() ,解出x即为原计划每天生产的零件个数,再代入
,解出x即为原计划每天生产的零件个数,再代入![]() 即可求得规定天数;(2)设原计划安排的工人人数为y人,根据“(5组机器人生产流水线每天生产的零件个数+原计划每天生产的零件个数)×(规定天数-2)=零件总数24000个”可列方程[5×20×(1+20%)×
即可求得规定天数;(2)设原计划安排的工人人数为y人,根据“(5组机器人生产流水线每天生产的零件个数+原计划每天生产的零件个数)×(规定天数-2)=零件总数24000个”可列方程[5×20×(1+20%)×![]() +2400] ×(10-2)=24000,解得y的值即为原计划安排的工人人数.
+2400] ×(10-2)=24000,解得y的值即为原计划安排的工人人数.
试题解析:(1)解:设原计划每天生产零件x个,由题意得,
![]() ,
,
解得x=2400,
经检验,x=2400是原方程的根,且符合题意.
∴规定的天数为24000÷2400=10(天).
答:原计划每天生产零件2400个,规定的天数是10天.
(2)设原计划安排的工人人数为y人,由题意得,
[5×20×(1+20%)×![]() +2400] ×(10-2)=24000,
+2400] ×(10-2)=24000,
解得,y=480.
经检验,y=480是原方程的根,且符合题意.
答:原计划安排的工人人数为480人.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于两点A,B,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为点D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).
(1)求抛物线的函数表达式;
(2)求点E的坐标;
(3)试探究在x轴下方的抛物线上是否存在点F,使得△FOB和△EOB的面积相等,若存在,请求出点F的坐标,若不存在,请说明理由;
(4)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,请直接写出:当m为何值时,△OPQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国有五座名山,但在洪雅人的心目中,我国有六座名山,这六座名山的海拔分别为:
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔(米) | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
(1)海拔最高的山是多少,最高的山与最低的山的海拔相差多少米;
(2)海拔不低于1500米的山的频数是多少;频率是多少;
(3)根据数据制作条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地.如图(2)是汽车行驶时离C站的路程y(千米)与行驶时间x(小时)之间的函数关系的图象.
(1)a等于多少km,AB两地的距离为多少km;
(2)求线段PM、MN所表示的y与x之间的函数表达式;
(3)求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习:
在一次数学兴趣小组活动中,老师和几个同学一起探讨:在an=b中,a,b,n三者关系.
同学甲:已知a,n,可以求b,是我们学过的乘方运算,其中b叫做a的n次方.如:(﹣2)3=﹣8,其中﹣8是﹣2的3次方.
同学乙:已知b,n,可以求a,是我们学过的开方运算,其中a叫做b的n次方根.如:(±2)2=4,其中±2 是4的二次方根(或平方根);(﹣3)3=﹣27,其中﹣3是﹣27的三次方根(或立方根).
老师:两位同学说的很好,那么请大家计算:
(1)81的四次方根等于 ;﹣32的五次方根等于 .
同学丙:老师,如果已知a和b,那么如何求n呢?又是一种什么运算呢?
老师:这个问题问的好,已知a,b,可以求n,它是一种新的运算,称为对数运算.
这种运算的定义是:若an=b(a>0,a≠1),n叫做以a为底b的对数,记作:n=logab.例如:23=8,3叫做 以2为底8的对数,记作3=log28.根据题意,请大家计算:
(2)log327= ; (![]() )﹣2+
)﹣2+![]() ﹣log4
﹣log4![]() = .
= .
随后,老师和同学们又一起探究出对数运算的一条性质:如果a>0,a≠1,M>0,N>0,那么logaMN=logaM+logaN.
(3)请你利用上述性质计算:log53+log5![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,![]() , C△ABC=10cm且∠C=60°.求:
, C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)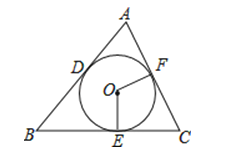
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:⊙O的直径AB=12,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C,设AD=X,BC=Y,求Y与X的函数关系式,并画出它的大致图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com