
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于两点A,B,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为点D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).
(1)求抛物线的函数表达式;
(2)求点E的坐标;
(3)试探究在x轴下方的抛物线上是否存在点F,使得△FOB和△EOB的面积相等,若存在,请求出点F的坐标,若不存在,请说明理由;
(4)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,请直接写出:当m为何值时,△OPQ是等腰三角形.
【答案】
(1)
解:将点A(﹣2,0)、D(6,﹣8)代入y=ax2+bx﹣8,
得: ![]() ,
,
解得: 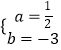 ,
,
∴抛物线的函数表达式为y= ![]() x2﹣3x﹣8
x2﹣3x﹣8
(2)
解:设直线l的解析式为y=kx,
将D(6,﹣8)代入,得:6k=﹣8,
解得:k=﹣ ![]() ,
,
∴直线l的解析式为y=﹣ ![]() x,
x,
又抛物线的对称轴为x=﹣ ![]() =3,
=3,
∴点E的坐标为(3,﹣4)
(3)
解:存在,
设点F(x, ![]() x2﹣3x﹣8),
x2﹣3x﹣8),
∵S△FOB=S△EOB,即 ![]() OByF=
OByF= ![]() OByE,
OByE,
∴yF=yE,即 ![]() x2﹣3x﹣8=﹣4,
x2﹣3x﹣8=﹣4,
解得:x=3± ![]() ,
,
∴点F的坐标为(3﹣ ![]() ,﹣4)或(3+
,﹣4)或(3+ ![]() ,﹣4)
,﹣4)
(4)
解:①如图1
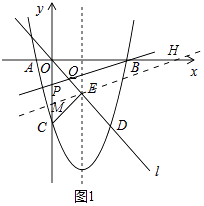
当OP=OQ时,△OPQ是等腰三角形.
∵点E坐标(3,﹣4),
∴OE= ![]() =5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则
=5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则 ![]() =
= ![]() ,
,
∴OM=OE=5,
∴点M坐标(0,﹣5).
设直线ME的解析式为y=k1x﹣5,
∴3k1﹣5=﹣4,
∴k1= ![]() ,
,
∴直线ME解析式为y= ![]() x﹣5,
x﹣5,
令y=0,得 ![]() x﹣5=0,解得x=15,
x﹣5=0,解得x=15,
∴点H坐标(15,0),
∵MH∥PB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴m=﹣ ![]() ,
,
②如图2,
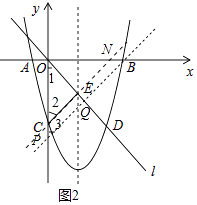
当QO=QP时,△POQ是等腰三角形.
∵当x=0时,y= ![]() x2﹣3x﹣8=﹣8,
x2﹣3x﹣8=﹣8,
∴点C坐标(0,﹣8),
∴CE= ![]() =5,
=5,
∴OE=CE,
∴∠1=∠2,
∵QO=QP,
∴∠1=∠3,
∴∠2=∠3,
∴CE∥PB,
设直线CE交x轴于N,解析式为y=k2x﹣8,
∴3k2﹣8=﹣4,
∴k2= ![]() ,
,
∴直线CE解析式为y= ![]() x﹣8,
x﹣8,
令y=0,得 ![]() x﹣8=0,
x﹣8=0,
∴x=6,
∴点N坐标(6,0),
∵CN∥PB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴m=﹣ ![]() .
.
③OP=PQ时,显然不可能,理由,
∵D(6,﹣8),
∴∠1<∠BOD,
∵∠OQP=∠BOQ+∠ABP,
∴∠PQO>∠1,
∴OP≠PQ,
综上所述,当m=﹣ ![]() 或﹣
或﹣ ![]() 时,△OPQ是等腰三角形
时,△OPQ是等腰三角形
【解析】(1)待定系数法求解可得;(2)求得直线l的解析式和抛物线对称轴即可得出交点坐标;(3)根据△FOB和△EOB共底且面积相等可得yF=yE , 即 ![]() x2﹣3x﹣8=﹣4,解之可得答案;(4)①如图1中,当OP=OQ时,△OPQ是等腰三角形,过点E作直线ME∥PB,交y轴于点M,交x轴于点H,求出点M、H的坐标即可解决问题.②如图2中,当QO=QP时,△POQ是等腰三角形,先证明CE∥PQ,根据平行线的性质列出方程即可解决问题.
x2﹣3x﹣8=﹣4,解之可得答案;(4)①如图1中,当OP=OQ时,△OPQ是等腰三角形,过点E作直线ME∥PB,交y轴于点M,交x轴于点H,求出点M、H的坐标即可解决问题.②如图2中,当QO=QP时,△POQ是等腰三角形,先证明CE∥PQ,根据平行线的性质列出方程即可解决问题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D. 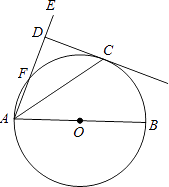
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半径;②求tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1, 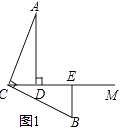
①线段CD和BE的数量关系是;
②请写出线段AD,BE,DE之间的数量关系 .
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系. 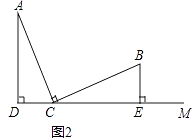
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,以BC为边作等边△BDC,连接AD.
(1)如图1,直接写出∠ADB的度数 ;
(2)如图2,作∠ABM=60°在BM上截取BE,使BE=BA,连接CE,判断CE与AD的数量关系,请补全图形,并加以证明;
(3)在(2)的条件下,连接DE,AE.若∠DEC=60°,DE=2,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一空间图形的三视图如下图所示,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的四分之一圆以及高为1的矩形;俯视图:半径为1的圆,求此图形的体积.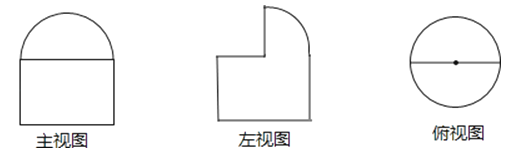
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中, ∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线. ①求证: ∠AFC=120°;②若AD=6,CE=4,求AC的长?
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
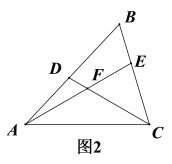
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com