
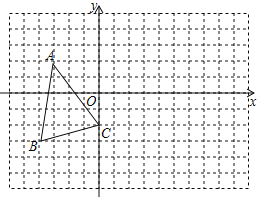
【题目】如图,已知在直角坐标系中,![]() 的顶点都在网络格上:
的顶点都在网络格上:
(1)请写出点![]() 的坐标;
的坐标;
(2)先画出![]() 先向
先向![]() 轴正方向平移
轴正方向平移![]() 个单位长度,得到
个单位长度,得到![]() ;请写出点
;请写出点![]() 的坐标.
的坐标.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( ) 
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.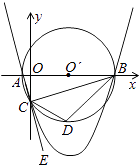
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在数轴上有A、 B两点,点A表示的数是-6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动,设运动时间为t秒.
(1) AB=____ ;当t=1时,点Q表示的数是___ ;当t=___时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由.若不变,请求出线段MN的长;
(3)如图3,若点M为线段的AP中点,点T为线段BQ中点,则点M表示的数为______;点T表示的数为______;MT=______ (用含t的代数式填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
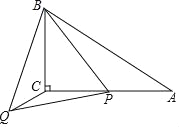
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com