搜索
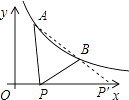
【题目】如图所示，已知A（ 
，y1），B（2，y2）为反比例函数y= 
图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
A.（ ，0）
B.（1，0）
C.（ 
，0）
D.（ 
，0）
参考答案：
【答案】D
【解析】解：∵把A（ 
，y1），B（2，y2）代入反比例函数y= 
得：y1=2，y2= ，
∴A（ ，2），B（2， ），
∵在△ABP中，由三角形的三边关系定理得：|AP﹣BP|＜AB，
∴延长AB交x轴于P′，当P在P′点时，PA﹣PB=AB，
即此时线段AP与线段BP之差达到最大，
设直线AB的解析式是y=kx+b，
把A、B的坐标代入得：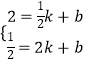 
，
解得：k=﹣1，b= 
，
∴直线AB的解析式是y=﹣x+ ，
当y=0时，x= ，
即P（ ，0），
故选：D．
【考点精析】关于本题考查的反比例函数的性质，需要了解性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
的图象经过点（﹣1，-2
），点A是该图象第一象限分支上的动点，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点D，当
=时，则点C的坐标为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于平面内的∠M和∠N，若存在一个常数k＞0，使得∠M＋k∠N＝360°，则称∠N为∠M的k系补周角．如若∠M＝90°，∠N＝45°，则∠N为∠M的6系补周角．
（1）若∠H＝120°，则∠H的4系补周角的度数为 ；
（2）在平面内AB∥CD，点E是平面内一点，连接BE，DE．
①如图1，∠D＝60°，若∠B是∠E的3系补周角，求∠B的度数；
②如图2，∠ABE和∠CDE均为钝角，点F在点E的右侧，且满足∠ABF=n∠ABE，∠CDF=n∠CDE（其中n为常数且n＞1），点P是∠ABE角平分线BG上的一个动点，在P点运动过程中，请你确定一个点P的位置，使得∠BPD是∠F的k系补周角，并直接写出此时的k值（用含n的式子表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈,以下各层均比上一层多一个圆圈，一共堆了
层，将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为
如果图中的圆圈共有13层，请解决下列问题：
(1)若自上往下，在图①每个圆圈中填上一串连续的正整数1，2，3，4，…，得到图3，写出第11层最左边这个圆圈中的数；
(2)若自上往下，在图①每个圆圈中填上一串连续的整数-23，-22，-21，20，…，得到图4，写出第10层最右边圆圈内的数；
(3)根据以上规律，求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于
MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（ ）.①作出AD的依据是SAS；②∠ADC=60°
③点D在AB的中垂线上；④S△DAC：S△ABD=1：2．
A.1B.2C.3D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知两个等腰直角△ABC和△CDE，它们的两个直角顶点B、D在直线MN上，过点A、E分别作AG⊥MN，EF⊥MN，垂足分别为G、F．
(1)如图1，当△ABC和△CDE在△BCD的外部时，请你探索线段EF、DB、AG之间的数量关系，其数量关系为______．
(2)如图2，将图1中的△ABC沿BC翻折，其他条件不变，那么(1)中的结论是否仍然成立？若成立，请你给出证明，若不成立，请探索它们的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线OD交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC度数为( ).
A. 108° B. 135° C. 144° D. 160°
相关试题
