
【题目】若方程 (m3)xm27x+3=0 是关于x的一元二次方程,则方程( )
A.无实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.有一个根
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AF∥DE,B为AF上一点,∠ABC=60°,交ED于C,CM平分∠BCE,∠MCN=90°.
(1)求∠DCN的度数;
(2)若∠CBF的平分线交CN于N,求证:BN∥CM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人(两人走的路线相同)?试求解这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB. 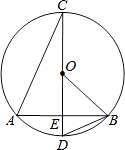
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分:
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 |
| 54 | 9 |

根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有多少人,这些学生数占被调查总人数的百分比为多少;
(2)被调查学生的总人数为多少人,统计表中![]() 的值为多少,统计图中
的值为多少,统计图中![]() 的值为多少;
的值为多少;
(3)求在统计图中,B类所对应扇形圆心角的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为_____厘米/秒.
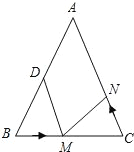
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A( ![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= ![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A.( ![]() ,0)
,0)
B.(1,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com