
【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A6B6C6的边长为 . 
【答案】![]()
【解析】解:作A2D1⊥A1B1于D1,A3D2⊥A2B2于D2,如图,
∵△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,
∴∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,
,
∴cos∠A2B1D1=cos30°= ![]() =
= ![]() ,
,
∴A2B1= ![]() ,
,
∵A2B1=B1B2,
∴A2B2= ![]() ,
,
同理可得∠A3B2D2=30°,B2D2= ![]() A2B2=
A2B2= ![]() ×
× ![]() =
= ![]() ,
,
∴cos∠A3B2D2=cos30°= ![]() =
= ![]() ,
,
∴A3B2= ![]() ,
,
∵A3B2=B2B3,
∴A3B3= ![]() =(
=( ![]() )2,
)2,
同理可得A4B4=( ![]() )3,
)3,
A5B5=( ![]() )4.A6B6C=(
)4.A6B6C=( ![]() )5=
)5= ![]() ,
,
故答案为 ![]() .
.
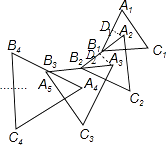
作A2D1⊥A1B1于D1,A3D2⊥A2B2于D2,根据等边三角形的中心的性质得∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,利用余弦的定义得cos∠A2B1D1=cos30°=
,利用余弦的定义得cos∠A2B1D1=cos30°= ![]() =
= ![]() ,可计算出A2B1=
,可计算出A2B1= ![]() ,由A2B1=B1B2得到A2B2=
,由A2B1=B1B2得到A2B2= ![]() ,用同样的方法可计算出A3B3=(
,用同样的方法可计算出A3B3=( ![]() )2,特殊的结论.
)2,特殊的结论.


科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人(两人走的路线相同)?试求解这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为_____厘米/秒.
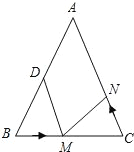
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A( ![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= ![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A.( ![]() ,0)
,0)
B.(1,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com