
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
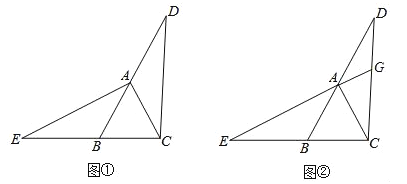
【题目】如图①.在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连接CD、AE.
(1)求证:△ACE≌△CBD;
(2)如图②,延长EA交CD于点G,则∠CGE的度数是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() 的“矩面积”,给出如下定义:“水平底”
的“矩面积”,给出如下定义:“水平底”![]() 是任意两点横坐标差的最大值;“铅垂高”
是任意两点横坐标差的最大值;“铅垂高”![]() 是任意两点纵坐标差的最大值,则“矩面积”
是任意两点纵坐标差的最大值,则“矩面积”![]() .例如:
.例如:![]() 三点的坐标分别为
三点的坐标分别为![]() ,则“水平底”
,则“水平底”![]() ,“铅垂高”
,“铅垂高”![]() ,“矩面积”
,“矩面积”![]() .根据所给定义解决下面的问题:
.根据所给定义解决下面的问题:
(1)若点![]() 的坐标分别为
的坐标分别为![]() ,求这三点的“矩面积”
,求这三点的“矩面积”![]() ;
;
(2)若点![]() ,含有
,含有![]() 的式子表示这三点的“矩面积”
的式子表示这三点的“矩面积”![]() (结果需化简);
(结果需化简);
(3)已知点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使这三点的“矩面积”
,使这三点的“矩面积”![]() 为20?若存在,求出点
为20?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( ) 
A.9
B.10
C.13
D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 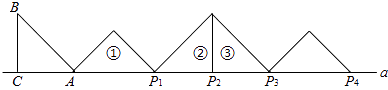
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com