
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() 的“矩面积”,给出如下定义:“水平底”
的“矩面积”,给出如下定义:“水平底”![]() 是任意两点横坐标差的最大值;“铅垂高”
是任意两点横坐标差的最大值;“铅垂高”![]() 是任意两点纵坐标差的最大值,则“矩面积”
是任意两点纵坐标差的最大值,则“矩面积”![]() .例如:
.例如:![]() 三点的坐标分别为
三点的坐标分别为![]() ,则“水平底”
,则“水平底”![]() ,“铅垂高”
,“铅垂高”![]() ,“矩面积”
,“矩面积”![]() .根据所给定义解决下面的问题:
.根据所给定义解决下面的问题:
(1)若点![]() 的坐标分别为
的坐标分别为![]() ,求这三点的“矩面积”
,求这三点的“矩面积”![]() ;
;
(2)若点![]() ,含有
,含有![]() 的式子表示这三点的“矩面积”
的式子表示这三点的“矩面积”![]() (结果需化简);
(结果需化简);
(3)已知点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使这三点的“矩面积”
,使这三点的“矩面积”![]() 为20?若存在,求出点
为20?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1) 21;(2) ![]() ;(3) (
;(3) (![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)根据题目中的新定义可以求得相应的“矩面积”;
(2)根据题目中的新定义可以求得相应的![]() ,h,可以求得相应的“矩面积”;
,h,可以求得相应的“矩面积”;
(3)设点F的坐标为(![]() ,0),再对
,0),再对![]() 进行分类讨论,即可求得
进行分类讨论,即可求得![]() 的值,从而可以求得点F的坐标.
的值,从而可以求得点F的坐标.
(1)∵点D(-1,2)、E(2,-1)、F(0,6),

∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:21;
(2)∵点D(2,3)、E(2,-1)、F(t,-2),

∴![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故答案为:![]() ;
;
(3)设点F的坐标为(![]() ,0),
,0),
∵点D(-1,2)、E(2,-2)、F(![]() ,0),
,0),
∴![]() ,
,
当点F在点D左侧时,![]() ,
,

根据题意:![]() ,
,
解得:![]() ,
,
∴点F的坐标为(![]() ,0),
,0),
当点F在点E右侧时,

![]() ,
,
根据题意:![]() ,
,
解得:![]() ,
,
∴点F的坐标为(![]() ,0),
,0),
当点F在点D、E之间,此时![]() ,
,
“矩面积”![]() ,
,
∴点F在点D、E之间时,不存在点F,使这三点的“矩面积”S为20,
综上,在![]() 轴上存在点
轴上存在点![]() ,使这三点的“矩面积”
,使这三点的“矩面积”![]() 为20,点F的坐标为(
为20,点F的坐标为(![]() ,0)或(
,0)或(![]() ,0) .
,0) .


科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE______DB(填“>”,“<”或“=”).
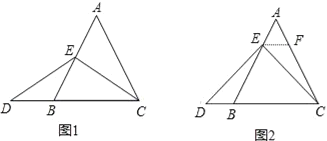
(2)一般情况,证明结论:
如图2,过点E作EF∥BC,交AC于点F.(请你继续完成对以上问题(1)中所填写结论的证明)
(3)拓展结论,设计新题:
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC. 若△ABC的边长为1,AE=2,则CD的长为_______(请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF.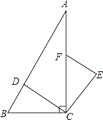
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )
A.有最大值 ![]()
B.有最大值﹣ ![]()
C.有最小值 ![]()
D.有最小值﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市投入15000元资金购进![]() 、
、![]() 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 | 成本价(元/箱) | 销售价(元/箱) |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
(1)该大型超市购进![]() 、
、![]() 品牌矿泉水各多少箱?
品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com