【题目】若一次函数y=（m+1）x+m的图象过第一、三、四象限，则函数y=mx2﹣mx（ ）
A.有最大值 
B.有最大值﹣
C.有最小值
D.有最小值﹣
【答案】B
【解析】解：∵一次函数y=（m+1）x+m的图象过第一、三、四象限，
∴m+1＞0，m＜0，
即﹣1＜m＜0，
∴函数y=mx2﹣mx=m（x﹣ 
）2﹣ 
有最大值，
∴最大值为﹣ ．
故选B．
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远，以及对二次函数的最值的理解，了解如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC、△ADE中，C、D两点分别在AE、AB上，BC、DE交于点F，若BD=DC=CE，∠ADC+∠ACD=114°，则∠DFC为（ ）
A.114°
B.123°
C.132°
D.147°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数y=ax﹣a（a为常数）的图象与y轴相交于点A，与函数y= 
的图象相交于点B（m，1）．
（1）求点B的坐标及一次函数的解析式；
（2）若点P在y轴上，且△PAB为直角三角形，请直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，对于任意三点
的“矩面积”，给出如下定义：“水平底”
是任意两点横坐标差的最大值；“铅垂高”
是任意两点纵坐标差的最大值，则“矩面积”
．例如：三点的坐标分别为
，则“水平底”
，“铅垂高”
，“矩面积”
．根据所给定义解决下面的问题：
（1）若点
的坐标分别为
，求这三点的“矩面积”
；
（2）若点
，含有
的式子表示这三点的“矩面积”(结果需化简)；
（3）已知点
，在
轴上是否存在点
，使这三点的“矩面积”为20？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
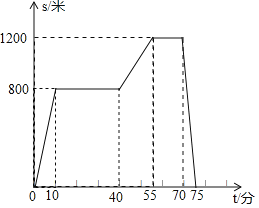
【题目】周六上午，小亮去图书馆查资料，图书馆离家不远，他步行去图书馆，查完资料后他又边走边转去书店买书，在书店停留了几分钟后骑共享单车回家．"已知小亮离家的距离
(米)与离开家的时间
(分)之间的关系如图所示．请根据图象回答下列问题：
（1）小亮出发几分钟后到达图书馆？
（2）小亮查完资料后步行的速度是多少？
（3）小亮
离开图书馆，几点回到家？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠A=60°，BD、BE三等分∠ABC，CD、CE三等分∠ACB，连接DE，则∠BDE=_____________°．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直线中相邻两条之间的距离依次为h1、h2、h3 ． 若h1=2，h2=1，则正方形ABCD的面积为（ ） 
A.9
B.10
C.13
D.25
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，火车站、码头分别位于A，B两点，直线a和b分别表示铁路与河流．
（1）从火车站到码头怎样走最近，画图并说明理由；
（2）从码头到铁路怎样走最近，画图并说明理由；
（3）从火车站到河流怎样走最近，画图并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】南昌的雾霾引起了小张对环保问题的重视．一次旅游小张思考了一个问题．从某地到南昌，若乘火车需要
小时，若乘汽车需要
小时．这两种交通工具平均每小时二氧化碳的排放量之和为
千克，火车全程二氧化碳的排放总量比汽车的多
千克，分别求火车和汽车平均每小时二氧化碳的排放量．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com