
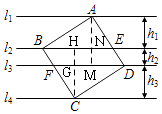
【题目】如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( ) 
A.9
B.10
C.13
D.25
【答案】C
【解析】证明:过A点作AM⊥l3分别交l2、l3于点N、M,过C点作CH⊥l2分别交l2、l3于点H、G,
∵四边形ABCD是正方形,l1∥l2∥l3∥l4,
∴AB=CD,∠ABN+∠HBC=90°,
∵CH⊥l2,
∴∠BCH+∠HBC=90°,
∴∠BCH=∠ABN,
∵∠BCH=∠CDG,
∴∠ABN=∠CDG,
∵∠ANB=∠CGD=90°,
在△ABN和△CDG中,
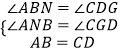 ,
,
∴△ABN≌△CDG(AAS),
∴AN=CG,BE=CH=h2+h3,
即h1=h3=2,BE=2+1=3,
在Rt△ABE中,由勾股定理得:AB2=AE2+BE2=22+32=13,
则正方形ABCD的面积=AB2=13;
故选C.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )
A.有最大值 ![]()
B.有最大值﹣ ![]()
C.有最小值 ![]()
D.有最小值﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有10名销售业务员,去年每人完成的销售额情况如表:

(1)求10名销售员销售额的平均数、中位数和众数.(单位:万元)
(2)为了调动员工积极性,公司准备采取超额有奖措施,请问把标准定为多少万元时最合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将抛物线 ![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为 ![]() ,与x轴的一个交点为A
,与x轴的一个交点为A ![]() ,另一交点为B,与y轴交点为C.
,另一交点为B,与y轴交点为C.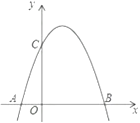
(1)求抛物线的函数表达式;
(2)若点 ![]() 为抛物线上一点,且BC⊥NC,求点N的坐标;
为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数 ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寿县教育部门计划在3月12日植树节当天安排![]() ,
,![]() 两校部分学生到森林公园参加植树活动.已知
两校部分学生到森林公园参加植树活动.已知![]() 校区的每位学生往返车费是6元,
校区的每位学生往返车费是6元,![]() 校每位学生的往返车费是10元,要求两所学校均要有学生参加,且
校每位学生的往返车费是10元,要求两所学校均要有学生参加,且![]() 校参加活动的学生比
校参加活动的学生比![]() 校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求
校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求![]() ,
,![]() 两校最多各有多少学生参加?
两校最多各有多少学生参加?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com