
【题目】如图,是将抛物线 ![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为 ![]() ,与x轴的一个交点为A
,与x轴的一个交点为A ![]() ,另一交点为B,与y轴交点为C.
,另一交点为B,与y轴交点为C.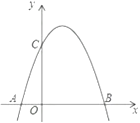
(1)求抛物线的函数表达式;
(2)若点 ![]() 为抛物线上一点,且BC⊥NC,求点N的坐标;
为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数 ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
【答案】
(1)解:设抛物线的解析式是 ![]() .
.
把 ![]() 代入得
代入得 ![]() ,解得,
,解得, ![]()
则抛物线的解析式是 ![]() ,即
,即 ![]() ;
;
(2)解:
方法一:设直线BC的解析式为 ![]() ,
,
![]()
∴直线BC的解析式为 ![]() ,
,
由BC⊥NC,则设直线CN的解析式为 ![]()
![]() ,即直线CN的解析式为
,即直线CN的解析式为 ![]()
∵N为直线BC与CN的交点,
∴联立方程得: ![]() ,即
,即 ![]() ,
,
∴ ![]() ,则N的坐标是
,则N的坐标是 ![]()
方法二:在 ![]() 中令
中令 ![]() ,则
,则 ![]() ,
,
即C的坐标是 ![]() ,OC=3.
,OC=3.
∵B的坐标是 ![]() ,
,
∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
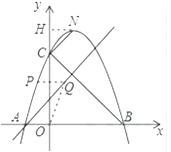
∵∠NCB=90°,∴∠NCH=45°,
∴NH=CH,∴HO=OC+CH=3+CH=3+NH,
设点N纵坐标是 ![]() .
.
∴ ![]() ,
,
解得 ![]() (舍去)或
(舍去)或 ![]() ,
,
∴N的坐标 ![]() ;
;
(3)解:∵四边形OAPQ是平行四边形,
则PQ=OA=1,且PQ∥OA,
设 ![]() ,则
,则 ![]() 代入
代入 ![]() ,
,
得 ![]() ,
,
整理,得 ![]() ,
,
解得 ![]() 或
或 ![]() .
.
∴ ![]() 的值为3或
的值为3或 ![]() .
.
∴P、Q的坐标是 ![]() 或
或 ![]() .
.
【解析】(1)由其对称轴为 x = 1 ,可得顶点横坐标为1,再由与x轴的一个交点为A ( 1 , 0 ),且由平移可得a=-1,所以易由顶点式求得解析式为y = x 2 + 2 x + 3
(2)由B(3,0)C(0,3)易得直线BC为y = x + 3 ,由于BC⊥NC,可得直线NC的斜率k=1,结合点C(0,3),可得到直线NC为y = x + 3;所求点N为二次函数与直线NC的交点,连列方程组可得N的坐标是 ( 1 , 4 )。
(3)由四边形OAPQ是平行四边形易得PQ=OA=1,且PQ∥OA,所以若设 P ( t , t 2 + 2 t + 3 ),则可得 Q ( t + 1 , t 2 + 2 t + 3 )由于Q为直线y = ![]() x +
x + ![]() 的点,代入可计算出t= 0 或 t =
的点,代入可计算出t= 0 或 t = ![]() ,代入所设 P ( t , t 2 + 2 t + 3 ), Q ( t + 1 , t 2 + 2 t + 3 ) 即可得两点坐标。
,代入所设 P ( t , t 2 + 2 t + 3 ), Q ( t + 1 , t 2 + 2 t + 3 ) 即可得两点坐标。
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数y= ![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1).
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( ) 
A.9
B.10
C.13
D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合中:-(-230),![]() ,0,-0.99,1.31,5,
,0,-0.99,1.31,5,![]() ,3.14246792…,-
,3.14246792…,-![]() .
.
(1)整数集合:{ …}
(2)非正数集合:{ …}
(3)正有理数集合:{ …}
(4)无理数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南昌的雾霾引起了小张对环保问题的重视.一次旅游小张思考了一个问题.从某地到南昌,若乘火车需要![]() 小时,若乘汽车需要
小时,若乘汽车需要![]() 小时.这两种交通工具平均每小时二氧化碳的排放量之和为
小时.这两种交通工具平均每小时二氧化碳的排放量之和为![]() 千克,火车全程二氧化碳的排放总量比汽车的多
千克,火车全程二氧化碳的排放总量比汽车的多![]() 千克,分别求火车和汽车平均每小时二氧化碳的排放量.
千克,分别求火车和汽车平均每小时二氧化碳的排放量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com