
【题目】如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE=_____________°.

【答案】50°
【解析】
根据三角形内角和为180°,设∠EBC=x,∠ECB=y,根据BD、BE三等分∠ABC,CD、CE三等分∠ACB,可得到∠BDC的度数,再得到DE是∠BDC角平分线即可求解.
∵在△ABC中,∠A=60°
∴∠ABC+∠ACB=180°-∠A=120°
设∠EBC=x,∠ECB=y,根据BD、BE三等分∠ABC,CD、CE三等分∠ACB,
∴3x+3y=120°
故x+y=40°,
∴∠DBC+∠DCB= 2x+2y=80°
∴在△DBC中,∠BDC=180°-(∠DBC+∠DCB)=100°
∵BE、CE是∠DBC、∠DCB的角平分线
∴DE是∠BDC的角平分线,
∴∠BDE=![]() ∠BDC=50°
∠BDC=50°
故答案为:50.


科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点按顺时针方向旋转90后得CE,连接EF.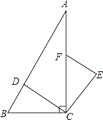
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )
A.有最大值 ![]()
B.有最大值﹣ ![]()
C.有最小值 ![]()
D.有最小值﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60,AB=3,求⊙P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3. 
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com