练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC、△ADE中，C、D两点分别在AE、AB上，BC、DE交于点F，若BD=DC=CE，∠ADC+∠ACD=114°，则∠DFC为（ ）

    A.114°
    B.123°
    C.132°
    D.147°

    【答案】B
    【解析】∵BD=CD=CE，等腰三角形的性质得出∠B=∠DCB，∠E=∠CDE，

    ∵∠ADC+∠ACD=114°，

    ∴∠BDC+∠ECD=360°﹣114°=246°，

    ∴∠B+∠DCB+∠E+∠CDE=360°﹣246°=114°，

    ∴∠DCB+∠CDE=57°，

    ∴∠DFC=180°﹣57°=123°，

    所以答案是：B．


    【考点精析】利用等腰三角形的性质对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】图象中所反应的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离，根据图象提供的信息，以下四个说法错误的是(　　)

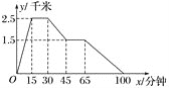
    A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟

    C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是千米/小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O中，点A为 中点，BD为直径，过A作AP∥BC交DB的延长线于点P．

    （1）求证：PA是⊙O的切线；
    （2）若 ，AB=6，求sin∠ABD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，李老师出示了如下框中的题目．

    小明与同桌小聪讨论后，进行了如下解答：

    （1）特殊情况，探索结论

    当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE______DB（填“＞”，“＜”或“=”）．

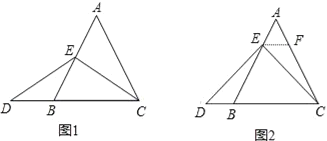
    （2）一般情况，证明结论：

    如图2，过点E作EF∥BC，交AC于点F．（请你继续完成对以上问题（1）中所填写结论的证明）

    （3）拓展结论，设计新题：

    在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC． 若△ABC的边长为1，AE=2，则CD的长为_______（请直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，铁路上A、B两点相距25km，C、D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA＝15km，CB＝10km，现在要在铁路AB上建一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多少千米处？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一电线杆AB的影子分别落在了地上和墙上．同一时刻，小明竖起1米高的直杆MN，量得其影长MF为0.5米，量得电线杆AB落在地上的影子BD长3米，落在墙上的影子CD的高为2米．你能利用小明测量的数据算出电线杆AB的高吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a、b、c满足|a﹣|++（c﹣4）2=0．

    （1）求a、b、c的值；

    （2）判断以a、b、c为边能否构成三角形？若能构成三角形，此三角形是什么形状？并求出三角形的面积；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是（ ）

    A. 10cm B. 12cm C. 15cm D. 17cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一次函数y=（m+1）x+m的图象过第一、三、四象限，则函数y=mx2﹣mx（ ）
    A.有最大值
    B.有最大值﹣
    C.有最小值
    D.有最小值﹣

    查看答案和解析>>

    同步练习册答案