
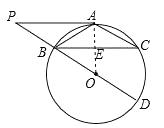
【题目】如图,⊙O中,点A为 ![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若 ![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
【答案】
(1)证明:连结AO,交BC于点E.
∵点A是 ![]() 的中点
的中点
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切线
(2)解:解:∵AO⊥BC, ![]() ,
,
∴ ![]() ,
,
又∵AB=6
∴sin∠BAO= ![]() ,
,
∵OA=OB
∴∠ABD=∠BAO,
∴ sin∠ABD=sin∠BAO= ![]() .
.
【解析】(1)由垂径定理可得AO⊥BC,再由AP∥BC,可得AP⊥AO,切线得证。
(2)由垂径定理易得BE的长,结合AB的长,易得sin∠BAO的值,再利用半径相等得到∠ABD=∠BAO,从而 sin∠ABD=sin∠BAO得到最后结果。
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人. 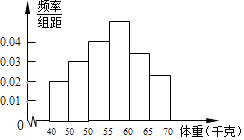
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE= ![]() AB;③S△ADE=
AB;③S△ADE= ![]() S△ABC . 正确的有( )
S△ABC . 正确的有( )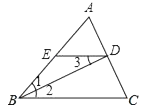
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.
(1)若∠CAE=∠B+30°,求∠B的大小;
(2)若AC=3,AB=5,求△AEB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个正n边形(n>4)的内角和是外角和的3倍,则n=;
B.小明站在教学楼前50米处,测得教学楼顶部的仰角为20°,测角仪的高度为1.5米,则此教学楼的高度为米.(用科学计算器计算,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
A.114°
B.123°
C.132°
D.147°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数y= ![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1).
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com