
【题目】如图,在ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.
(1)若∠CAE=∠B+30°,求∠B的大小;
(2)若AC=3,AB=5,求△AEB的周长.

【答案】(1)∠B=20°;(2)△AEB的周长=11.25.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,根据等边对等角可得∠B=∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CEA=∠B+∠BAE=2∠B,然后在△ACE中,根据直角三角形两锐角互余列出方程求解即可;
(2)利用勾股定理列式求出BC=4,设AE=BE=x,表示出CE=4﹣x,然后在Rt△ACE中,利用勾股定理列式求出x,再根据三角形的周长的定义列式计算即可得解.
解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠BAE,
∴∠CEA=∠B+∠BAE=2∠B,
在△ACE中,∠CAE+∠CEA=∠B+30°+2∠B=90°,
解得∠B=20°;
(2)由勾股定理得,![]() =4,
=4,
设AE=BE=x,则CE=4﹣x,
在Rt△ACE中,AC2+CE2=AE2,
即32+(4﹣x)2=x2,
解得x=![]() ,
,
∴△AEB的周长=![]() ×2+5=11.25.
×2+5=11.25.


科目:初中数学 来源: 题型:
【题目】一辆汽车在直线形的公路上由A向B行驶,M、N分别是位于公路AB两侧的两个学校,如图.
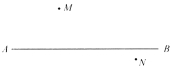
(1)汽车行驶时,会对公路两旁的学校都造成一定的影响,当汽车行驶到何处时,分别对两个学校影响最大?在图中标出来;
(2)当汽车从A向B行驶时,在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△A'B'C'关于直线m对称.
(1)结合图形指出对称点;
(2)若连接AA',直线m与线段AA'有什么关系?
(3)BC与B'C'的交点,AB与A'B'的交点分别与直线m有怎样的关系?若延长AC与A'C',其交点与直线m有怎样的关系?你发现了什么规律?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y. 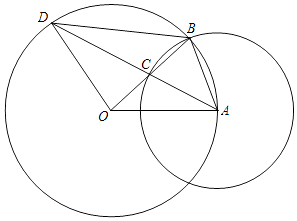
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,点A为 ![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若 ![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,射线
,射线![]() 从
从![]() 位置起始,绕点
位置起始,绕点![]() 逆时针旋转,终边
逆时针旋转,终边![]() 与始边
与始边![]() 形成的角度为
形成的角度为![]() .
.
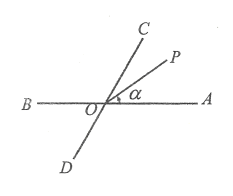
问题1:若![]() 逆时针旋转
逆时针旋转![]() 停止,则
停止,则
(1)![]() __________________时,
__________________时,![]() 平分
平分![]() ;
;
(2)![]() __________________时,
__________________时,![]() ;
;
(3)![]() __________________时,
__________________时,![]() ;
;
问题2:若![]() 逆时针旋转的速度为每秒
逆时针旋转的速度为每秒![]() ,在
,在![]() 匀速旋转的同时,直线
匀速旋转的同时,直线![]() 也从图的位置开始绕点
也从图的位置开始绕点![]() 逆时针匀速旋转,旋转速度为每秒
逆时针匀速旋转,旋转速度为每秒![]() ,当
,当![]() 完成旋转一周时,
完成旋转一周时,![]() 也同时停止旋转.设旋转时间为
也同时停止旋转.设旋转时间为![]() (
(![]() )秒.
)秒.
(1)旋转时间![]() 为多少时,射线
为多少时,射线![]() 与
与![]() 重合.请写出求解过程.
重合.请写出求解过程.
(2)观察旋转全过程,判断旋转时间![]() 为多少时,射线
为多少时,射线![]() 平分
平分![]() .请直接写出
.请直接写出![]() 的值.(注:
的值.(注:![]() 指大于
指大于![]() 且小于
且小于![]() 的角)
的角)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com