
”¾ĢāÄæ”æŹżŃ§æĪÉĻ£¬ĄīĄĻŹ¦³öŹ¾ĮĖČēĻĀæņÖŠµÄĢāÄ森

Š”Ć÷ÓėĶ¬×ĄŠ”“ĻĢÖĀŪŗ󣬽ųŠŠĮĖČēĻĀ½ā“š£ŗ
£Ø1£©ĢŲŹāĒéæö£¬Ģ½Ė÷½įĀŪ
µ±µćEĪŖABµÄÖŠµćŹ±£¬ČēĶ¼1£¬Č·¶ØĻ߶ĪAEÓėDBµÄ“󊔹ŲĻµ£¬ĒėÄćÖ±½ÓŠ“³ö½įĀŪ£ŗAE______DB£ØĢī”°£¾”±£¬”°£¼”±»ņ”°=”±£©£®
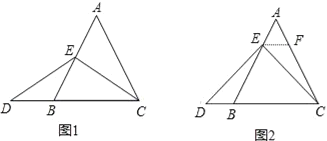
£Ø2£©Ņ»°ćĒéæö£¬Ö¤Ć÷½įĀŪ£ŗ
ČēĶ¼2£¬¹żµćE×÷EF”ĪBC£¬½»ACÓŚµćF£®£ØĒėÄć¼ĢŠųĶź³É¶ŌŅŌÉĻĪŹĢā£Ø1£©ÖŠĖłĢīŠ“½įĀŪµÄÖ¤Ć÷£©
£Ø3£©ĶŲÕ¹½įĀŪ£¬Éč¼ĘŠĀĢā£ŗ
ŌŚµČ±ßČż½ĒŠĪABCÖŠ£¬µćEŌŚÖ±ĻßABÉĻ£¬µćDŌŚÖ±ĻßBCÉĻ£¬ĒŅED=EC£® Čō”÷ABCµÄ±ß³¤ĪŖ1£¬AE=2£¬ŌņCDµÄ³¤ĪŖ_______£ØĒėÖ±½ÓŠ“³ö½į¹ū£©£®
”¾“š°ø”æ£Ø1£©=£»£Ø2£©=£»£Ø3£©1»ņ3£®
”¾½āĪö”æ
£Ø1£©µ±EĪŖÖŠµćŹ±£¬¹żE×÷EF”ĪBC½»ACÓŚµćF£¬ŌņæÉÖ¤Ć÷”÷BDE”Õ”÷FEC£¬æɵƵ½AE=DB£»
£Ø2£©ĄąĖĘ£Ø1£©¹żE×÷EF”ĪBC½»ACÓŚµćF£¬æÉĄūÓĆAASÖ¤Ć÷”÷BDE”Õ”÷FEC£¬æɵĆBD=EF£¬ŌŁÖ¤Ć÷”÷AEFŹĒµČ±ßČż½ĒŠĪ£¬æɵƵ½AE=EF£¬æɵĆAE=DB£»
£Ø3£©·ÖĪŖĖÄÖÖĒéæö£ŗ»³öĶ¼ŠĪ£¬øł¾ŻµČ±ßČż½ĒŠĪŠŌÖŹĒó³ö·ūŗĻĢõ¼žµÄCD¼“æÉ£®
½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żµćE×÷EF”ĪBC£¬½»ACÓŚµćF£¬

”ß”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻAFE=”ĻACB=”ĻABC=60”ć£¬”÷AEFĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻEFC=”ĻEBD=120”ć£¬EF=AE£¬
”ßED=EC£¬
”ą”ĻEDB=”ĻECB£¬”ĻECB=”ĻFEC£¬
”ą”ĻEDB=”ĻFEC£¬
ŌŚ”÷BDEŗĶ”÷FECÖŠ£¬

”ą”÷BDE”Õ”÷FEC£ØAAS£©£¬
”ąBD=EF£¬
”ąAE=BD£¬
¹Ź“š°øĪŖ£ŗ=£»
£Ø2£©ČēĶ¼2£¬¹żµćE×÷EF”ĪBC£¬½»ACÓŚµćF£¬
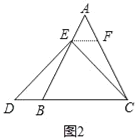
”ß”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻAFE=”ĻACB=”ĻABC=60”ć£¬”÷AEFĪŖµČ±ßČż½ĒŠĪ£¬
”ą”ĻEFC=”ĻEBD=120”ć£¬EF=AE£¬
”ßED=EC£¬
”ą”ĻEDB=”ĻECB£¬”ĻECB=”ĻFEC£¬
”ą”ĻEDB=”ĻFEC£¬
ŌŚ”÷BDEŗĶ”÷FECÖŠ

”ą”÷BDE”Õ”÷FEC£ØAAS£©£¬
”ąBD=EF£¬
”ąAE=BD£®
£Ø3£©½ā£ŗ·ÖĪŖĖÄÖÖĒéæö£ŗ
ČēĶ¼3£¬
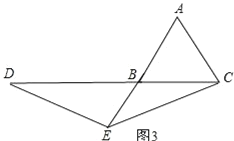
”ßAB=AC=1£¬AE=2£¬
”ąBŹĒAEµÄÖŠµć£¬
”ß”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬
”ąAB=AC=BC=1£¬”÷ACEŹĒÖ±½ĒČż½ĒŠĪ£Øøł¾ŻÖ±½ĒČż½ĒŠĪŠ±±ßµÄÖŠĻßµČÓŚŠ±±ßµÄŅ»°ė£©£¬
”ą”ĻACE=90”ć£¬”ĻAEC=30”ć£¬
”ą”ĻD=”ĻECB=”ĻBEC=30”ć£¬”ĻDBE=”ĻABC=60”ć£¬
”ą”ĻDEB=180”ć©30”ć©60”ć=90”ć£¬
¼“”÷DEBŹĒÖ±½ĒČż½ĒŠĪ£®
”ąBD=2BE=2£Ø30”ćĖł¶ŌµÄÖ±½Ē±ßµČÓŚŠ±±ßµÄŅ»°ė£©£¬
¼“CD=1+2=3£®
ČēĶ¼4£¬
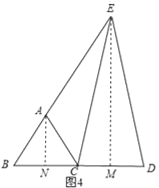
¹żA×÷AN”ĶBCÓŚN£¬¹żE×÷EM”ĶCDÓŚM£¬
”ߵȱßČż½ĒŠĪABC£¬EC=ED£¬
”ąBN=CN=![]() BC=
BC=![]() £¬CM=MD=
£¬CM=MD=![]() CD£¬AN”ĪEM£¬
CD£¬AN”ĪEM£¬
”ą”÷BAN”×”÷BEM£¬
”ą![]() £¬
£¬
”ß”÷ABC±ß³¤ŹĒ1£¬AE=2£¬
”ą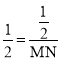 £¬
£¬
”ąMN=1£¬
”ąCM=MN©CN=1©![]() =
=![]() £¬
£¬
”ąCD=2CM=1£»
ČēĶ¼5£¬

”ß”ĻECD£¾”ĻEBC£Ø”ĻEBC=120”ć£©£¬¶ų”ĻECD²»ÄÜ“óÓŚ120”ć£¬·ńŌņ”÷EDC²»·ūŗĻČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķ£¬
”ą“ĖŹ±²»“ęŌŚEC=ED£»
ČēĶ¼6£¬
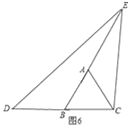
”ß”ĻEDC£¼”ĻABC£¬”ĻECB£¾”ĻACB£¬
Ó֔ߔĻABC=”ĻACB=60”ć£¬
”ą”ĻECD£¾”ĻEDC£¬
¼““ĖŹ±ED”ŁEC£¬
”ą“ĖŹ±Ēéæö²»“ęŌŚ£¬
“š£ŗCDµÄ³¤ŹĒ3»ņ1£®
¹Ź“š°øĪŖ£ŗ1»ņ3£®


 ±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßBC”¢CDÉĻ£¬”÷AEFŹĒµČ±ßČż½ĒŠĪ£¬Čē¹ūAB=1£¬ÄĒĆ“CEµÄ³¤ŹĒ£® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻA=40”ć£¬”ĻB=70”ć£¬CEĘ½·Ö”ĻACB£¬CD”ĶABÓŚD£¬DF”ĶCE£¬Ōņ”ĻCDF= ¶Č£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĒė“ÓŅŌĻĀĮ½øöŠ”ĢāÖŠČĪŃ”Ņ»øö×÷“š£¬Čō¶ąŃ”£¬Ōņ°“µŚŅ»Ģā¼Ę·Ö£®
A£®Ņ»øöÕżn±ßŠĪ£Øn£¾4£©µÄÄŚ½ĒŗĶŹĒĶā½ĒŗĶµÄ3±¶£¬Ōņn=£»
B£®Š”Ć÷Õ¾ŌŚ½ĢѧĀ„Ē°50Ćד¦£¬²āµĆ½ĢѧĀ„¶„²æµÄŃö½ĒĪŖ20”ć£¬²ā½ĒŅĒµÄø߶ČĪŖ1.5Ć×£¬Ōņ“Ė½ĢѧĀ„µÄø߶ČĪŖĆ×£®£ØÓĆæĘѧ¼ĘĖćĘ÷¼ĘĖć£¬½į¹ū¾«Č·µ½0.1Ć×£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬”÷ABCŹĒ±ß³¤3cmµÄµČ±ßČż½ĒŠĪ£¬¶ÆµćP”¢QĶ¬Ź±“ÓA”¢BĮ½µć³ö·¢£¬·Ö±šŃŲAB”¢BC·½ĻņŌČĖŁŅĘ¶Æ£¬ĖüĆĒµÄĖŁ¶Č¶¼ŹĒ1cm/s£¬µ±µćPµ½“ļµćBŹ±£¬P”¢QĮ½µćĶ£Ö¹ŌĖ¶Æ£®ÉčµćPµÄŌĖ¶ÆŹ±¼äĪŖt£Øs£©£¬½ā“šĪŹĢā£ŗµ±tĪŖŗĪÖµŹ±£¬”÷PBQŹĒÖ±½ĒČż½ĒŠĪ?

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĶ¼£¬»Ų“šĪŹĢā£®
(1)·“Ó³ĮĖÄÄĮ½øö±äĮæÖ®¼äµÄ¹ŲĻµ£æ
(2)µćA£¬B·Ö±š±ķŹ¾Ź²Ć“£æ
(3)ĖµŅ»ĖµĖŁ¶ČŹĒŌõŃłĖꏱ¼ä±ä»Æ¶ų±ä»ÆµÄ£»
(4)ÄćÄÜÕŅµ½Ņ»øöŹµ¼ŹĒé¾³£¬“óÖĀ·ūŗĻĻĀĶ¼ĖłæĢ»µÄ¹ŲĻµĀš£æ
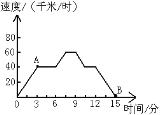
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABC”¢”÷ADEÖŠ£¬C”¢DĮ½µć·Ö±šŌŚAE”¢ABÉĻ£¬BC”¢DE½»ÓŚµćF£¬ČōBD=DC=CE£¬”ĻADC+”ĻACD=114”ć£¬Ōņ”ĻDFCĪŖ£Ø £©
A.114”ć
B.123”ć
C.132”ć
D.147”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£®ŌŚ”÷ABCÖŠ£¬AB£½AC£¬”ĻABC£½60”ć£¬ŃÓ³¤BAÖĮµćD£¬ŃÓ³¤CBÖĮµćE£¬Ź¹BE£½AD£¬Į¬½ÓCD”¢AE£®
£Ø1£©ĒóÖ¤£ŗ”÷ACE”Õ”÷CBD£»
£Ø2£©ČēĶ¼¢Ś£¬ŃÓ³¤EA½»CDÓŚµćG£¬Ōņ”ĻCGEµÄ¶ČŹżŹĒ”” ””¶Č£®
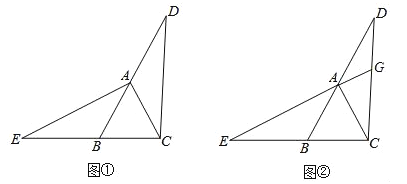
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬¶ŌÓŚČĪŅāČżµć
ÖŠ£¬¶ŌÓŚČĪŅāČżµć![]() µÄ”°¾ŲĆ껿”±£¬øų³öČēĻĀ¶ØŅå£ŗ”°Ė®Ę½µ×”±
µÄ”°¾ŲĆ껿”±£¬øų³öČēĻĀ¶ØŅå£ŗ”°Ė®Ę½µ×”±![]() ŹĒČĪŅāĮ½µćŗį×ų±ź²īµÄ×ī“óÖµ£»”°Ē¦“¹øß”±
ŹĒČĪŅāĮ½µćŗį×ų±ź²īµÄ×ī“óÖµ£»”°Ē¦“¹øß”±![]() ŹĒČĪŅāĮ½µćׯ×ų±ź²īµÄ×ī“óÖµ£¬Ōņ”°¾ŲĆ껿”±
ŹĒČĪŅāĮ½µćׯ×ų±ź²īµÄ×ī“óÖµ£¬Ōņ”°¾ŲĆ껿”±![]() £®ĄżČē£ŗ
£®ĄżČē£ŗ![]() ČżµćµÄ×ų±ź·Ö±šĪŖ
ČżµćµÄ×ų±ź·Ö±šĪŖ![]() £¬Ōņ”°Ė®Ę½µ×”±
£¬Ōņ”°Ė®Ę½µ×”±![]() £¬”°Ē¦“¹øß”±
£¬”°Ē¦“¹øß”±![]() £¬”°¾ŲĆ껿”±
£¬”°¾ŲĆ껿”±![]() £®øł¾ŻĖłøų¶ØŅå½ā¾öĻĀĆęµÄĪŹĢā£ŗ
£®øł¾ŻĖłøų¶ØŅå½ā¾öĻĀĆęµÄĪŹĢā£ŗ
£Ø1£©Čōµć![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() £¬ĒóÕāČżµćµÄ”°¾ŲĆ껿”±
£¬ĒóÕāČżµćµÄ”°¾ŲĆ껿”±![]() £»
£»
£Ø2£©Čōµć![]() £¬ŗ¬ÓŠ
£¬ŗ¬ÓŠ![]() µÄŹ½×Ó±ķŹ¾ÕāČżµćµÄ”°¾ŲĆ껿”±
µÄŹ½×Ó±ķŹ¾ÕāČżµćµÄ”°¾ŲĆ껿”±![]() (½į¹ūŠč»Æ¼ņ)£»
(½į¹ūŠč»Æ¼ņ)£»
£Ø3£©ŅŃÖŖµć![]() £¬ŌŚ
£¬ŌŚ![]() ÖįÉĻŹĒ·ń“ęŌŚµć
ÖįÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹ÕāČżµćµÄ”°¾ŲĆ껿”±
£¬Ź¹ÕāČżµćµÄ”°¾ŲĆ껿”±![]() ĪŖ20£æČō“ęŌŚ£¬Ēó³öµć
ĪŖ20£æČō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com