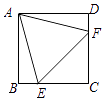
【题目】如图，在正方形ABCD中，点E、F分别在边BC、CD上，△AEF是等边三角形，如果AB=1，那么CE的长是． 
【答案】
﹣1
【解析】解：∵四边形正方形ABCD，
∴∠B=∠D=90°，AB=AD，
∵△AEF是等边三角形，
∴AE=EF=AF，
∴△ABE≌△ADF，
∴BE=DF，
设BE=x，那么DF=x，CE=CF=1﹣x，
在Rt△ABE中，AE2=AB2+BE2，
在Rt△EFC中，FE2=CF2+CE2，
∴AB2+BE2=CF2+CE2，
∴x2+1=2（1﹣x）2，
∴x2﹣4x+1=0，
∴x=2± 
，而x＜1，
∴x=2﹣ ，
即BE的长为=2﹣ ，
∴CE=BC﹣BE=1﹣（2﹣ ）= ﹣1．
【考点精析】根据题目的已知条件，利用等边三角形的性质和正方形的性质的相关知识可以得到问题的答案，需要掌握等边三角形的三个角都相等并且每个角都是60°；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
科目：初中数学 来源： 题型：
【题目】小亮调查本班同学的身高后,将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值.比如,第二小组数据x满足:145≤x<150,其他小组的数据类似).设班上学生身高的平均数为
,则的取值范围是____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（ ）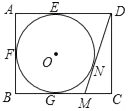
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
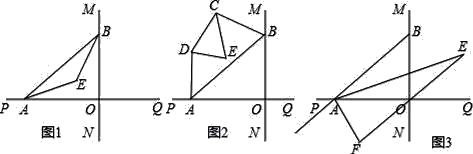
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，点E，F分别在BC，AC上，且BE=CF，连结AE与BF相交于点G．将△ABC沿AB边折叠得到△ABD，连结DG．延长EA到点H，使得AH=BG，连结DH．
（1）求证：四边形DBCA是菱形．
（2）若菱形DBCA的面积为8 
， 
，求△DGH的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于三个数
，用
表示这三个数中最大数，例如：
，
解决问题：
（1）填空：
{
，
，
}= ，如果{，
，
}=，则
的取值范围为 ；
（2）如果{，
，
}=
，求的值；
（3）如图，在同一坐标系中画出了三个一次函数的图象：
，
和
请观察这三个函数的图象，
①在图中画出{
，
，
}对应的图像（加粗）；
②{，
，}的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图象中所反应的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离，根据图象提供的信息，以下四个说法错误的是( )
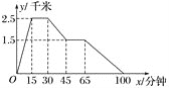
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是
千米/小时
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，三角形DEF是三角形ABC平移所得，观察图形：(1)点A的对应点是点 ，点B的对应点是点 ，点C的对应点是点 ；(2)线段AD，BE，CF叫做对应点间的连线，这三条线段之间有什么关系呢？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学课上，李老师出示了如下框中的题目．
小明与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE______DB（填“＞”，“＜”或“=”）．
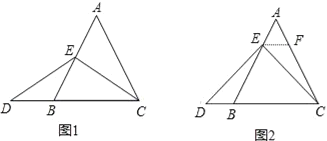
（2）一般情况，证明结论：
如图2，过点E作EF∥BC，交AC于点F．（请你继续完成对以上问题（1）中所填写结论的证明）
（3）拓展结论，设计新题：
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC． 若△ABC的边长为1，AE=2，则CD的长为_______（请直接写出结果）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com