
【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
【答案】(1)![]() ;
;![]() ;
;![]() (2)作图见详解,CH=
(2)作图见详解,CH=![]() (3)作图见详解
(3)作图见详解
【解析】
(1)根据勾股定理分别进行求解计算即可;(2)结合网格特点和三角形高的概念作图可得.
解:(1)由题意可得:![]()
![]()
![]()
故答案为:![]() ;
;![]() ;
;![]()
(2)如图,连接格点E,F,
∵AE=MF,∠AEB=∠FME,BE=EM
∴△EMF≌△BEA
∴∠MEF=∠EBA
又∵∠EBA+∠EAB=90°
∴∠MEF+∠EAB=90°
∴EF⊥AB
将EF向下平移2个单位,得到CH,
CH即为所求
由题意可知:![]()
![]()
∴![]()
解得:CH=![]()
故答案为:![]() ;
;

(3)由(2)已知CH⊥AB
与(2)同理连接BF,向右平移1个单位可得AM⊥BC
CH与AM的交点D即为△ABC的垂心,连接BD交AC于点G
BG即为所求



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空.
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD( ).
∴∠B=∠DCE( ).
又∵∠B=∠D(已知 ),
∴___________ ( 等量代换 ).
∴AD∥BE(内错角相等,两直线平行)
∴∠E=∠DFE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
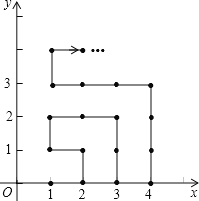
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知∠1+∠2=180°,∠2=∠B,试说明∠DEC+∠C=180°,请完成下列填空:

证明:∵∠1+∠2=180°(已知)
∴_____∥_____(____________________)
∴______=∠EFC(____________________)
又∵2=∠B(已知)
∴∠2=______(等量代换)
∴___________(内错角相等,两直线平行)
∴∠DEC+∠C=180°(两直线平行,同旁内角互补)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 ![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 ![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com