
【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 ![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 ![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
【答案】B
【解析】解:①∵五方形ABCDE是正五边形,
∴AB=BC,∠ABC=180°﹣ ![]() =108°,
=108°,
∴∠BAC=∠ACB=36°,
∴∠ACD=108°﹣36°=72°,
同理得:∠ADE=36°,
∵∠BAE=108°,AB=AE,
∴∠ABE=36°,
∴∠CBF=108°﹣36°=72°,
∴BC=FC,
∵BC=CD,
∴CD=CF,
∴∠CDF=∠CFD= ![]() =54°,
=54°,
∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
所以①正确;
②∵∠ABE=∠ACB=36°,∠BAC=∠BAF,
∴△ABF∽△ACB,
∴ ![]() ,
,
∴ABED=ACEG,
∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,
∴22=(2﹣FG)(4﹣FG),
∴FG=3+ ![]() >2(舍),FG=3﹣
>2(舍),FG=3﹣ ![]() ;
;
所以②正确;
③如图1,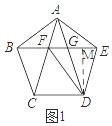
∵∠EBC=72°,∠BCD=108°,
∴∠EBC+∠BCD=180°,
∴EF∥CD,
∵EF=CD=2,
∴四边形CDEF是平行四边形,
过D作DM⊥EG于M,
∵DG=DE,
∴EM=MG= ![]() EG=
EG= ![]() (EF﹣FG)=
(EF﹣FG)= ![]() (2﹣3+
(2﹣3+ ![]() )=
)= ![]() ,
,
由勾股定理得:DM= ![]() =
= ![]() =
= ![]() ,
,
∴(S四边形CDEF)2=EF2DM2=4× ![]() =10+2
=10+2 ![]() ;
;
所以③不正确;
④如图2,连接EC,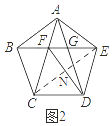
∵EF=ED,
∴CDEF是菱形,
∴FD⊥EC,
∵EC=BE=4﹣FG=4﹣(3﹣ ![]() )=1+
)=1+ ![]() ,
,
∴S四边形CDEF= ![]() FDEC=2×
FDEC=2× ![]() ,
,![]() ×FD×(1+
×FD×(1+ ![]() )=
)= ![]() ,
,
FD2=10﹣2 ![]() ,
,
∴DF2﹣DG2=10﹣2 ![]() ﹣4=6﹣2
﹣4=6﹣2 ![]() ,
,
所以④不正确;
本题正确的有两个,
故答案为:B.
①根据正五边形的性质证明△ABC,△ABE,△ADE是等腰三角形,求出∠ABC,∠ACB,∠BCD,∠CDE及∠ADE的度数,再证明CD=CF,根据等边对等角得出∠CDF=∠CFD=54°,然后根据∠FDG=∠CDE﹣∠CDF﹣∠ADE,计算即可求出∠FDG的度数,可对①作出判断;②先利用相似三角形的判定证明△ABF∽△ACB,得出ABED=ACEG,建立方程求出FG的长,就可对②作出判断;③先根据已知证明四边形CDEF是平行四边形,过D作DM⊥EG于M,求出EM的长,再利用勾股定理求出DM的长,然后求出(S四边形CDEF)2的值,可对③作出判断;④根据菱形的判断方法证明CDEF是菱形,得出FD⊥EC,求出EC的长,再根据菱形的面积公式建立方程求出FD2的长,然后求出DF2﹣DG2即可,就可对④作出判断;即可得出答案。


科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,线段![]() 直线
直线![]() ,垂足为
,垂足为![]() ,平移线段
,平移线段![]() ,使点
,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点记为点
的对应点记为点![]() .
.

操作与思考:
(1)画出线段![]() 和直线
和直线![]() ;
;
(2)直线![]() 与
与![]() 的位置关系是_______,理由是:____________________________;
的位置关系是_______,理由是:____________________________;
线段![]() 与
与![]() 的数量关系是_______,理由是:____________________________.
的数量关系是_______,理由是:____________________________.
实践与应用:
(3)如图,等边![]() 和等边
和等边![]() 的面积分别为3和5,点
的面积分别为3和5,点![]() 、
、![]() 、
、![]() 在一直线上,则
在一直线上,则![]() 的面积是_____________.
的面积是_____________.

(4)如图,网格中每个小正方形的边长为1,请用三种不同方法,求出![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.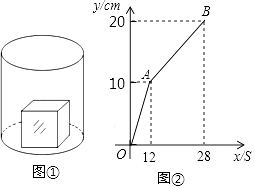
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
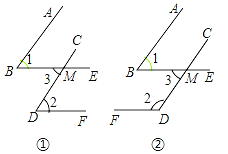
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(![]() ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com