
����Ŀ����֪����ͼ��ֱ��a��b��ֱ��c��ֱ��a��b�ֱ��ཻ��C��D���㣬ֱ��d��ֱ��a��b�ֱ��ཻ��A��B���㣬��P��ֱ��AB���˶�(����A��B�����غ�)��
(1)��ͼ1������P���߶�AB���˶�ʱ�����У���CPD����PCA+��PDB����˵�����ɣ�
(2)��ͼ2������P���߶�AB���ӳ������˶�ʱ����CPD����PCA����PDB֮����������������ϵ����˵�����ɣ�
(3)��ͼ3������P���߶�BA���ӳ������˶�ʱ����CPD����PCA����PDB֮������������������ϵ(ֻ��ֱ�Ӹ�������)��

���𰸡���1��֤������������2����CPD=��PCA����PDB�����ɼ���������3����CPD=��PDB����PCA��
��������
��1������P��a��ƽ���ߣ�����ƽ���ߵ����ʽ�����⣻
��2������P��b��ƽ����PE����ƽ���ߵ����ʿɵó�a��b��PE���ɴ˼��ɵó����ۣ�
��3����ֱ��AC��DP���ڵ�F������������ǵ����ʿɵó���1+��3=��PFA������ƽ���ߵ����ʼ��ɵó����ۣ�
��1��֤������ͼ1������P��PE��a�����1=��CPE��
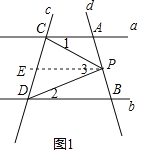
��a��b��PE��a��
��PE��b��
���2=��DPE��
���3=��1+��2��
����CPD=��PCA+��PDB��
��2����CPD=��PCA-��PDB��
���ɣ���ͼ2������P��PE��b�����2=��EPD��
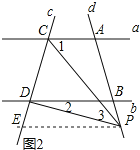
��ֱ��a��b��
��a��PE��
���1=��EPC��
�ߡ�3=��EPC-��EPD��
���3=��1-��2��
����CPD=��PCA-��PDB��
��3����CPD=��PDB-��PCA��
֤������ͼ3����ֱ��AC��DP���ڵ�F��
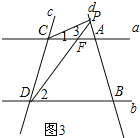
�ߡ�PFA����PCF����ǣ�
���PFA=��1+��3��
��a��b��
���2=��PFA��
���2=��1+��3��
���3=��2-��1��
����CPD=��PDB-��PCA��


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������PO���O����A��B���㣬PC��PD�ֱ��С�O�ڵ�C��D��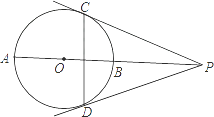
��1����д��������ͬ���͵���ȷ���ۣ�
��2����CD=12��tan��CPO= ![]() ����PO�ij���
����PO�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������ɸ���������ֱ�Ϊ�����ĵ㣬��˳��ͼ���������������У��磨1��0������2��0������2��1������1��1������1��2������2��2��������������������ɣ���2019���������Ϊ______��
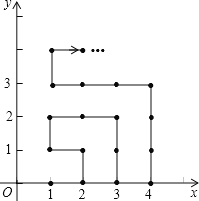
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F

��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ��������ӳ�Ĺ����ǣ���ǿ�Ӽ��ܲ�ȥ�������������������һ����� ȥ��͵����ͣ�Ȼ��ɢ���ؼң����� x ��ʾʱ�䣬y ��ʾ��ǿ��ҵľ��롣����ͼ���ṩ����Ϣ�������ĸ�˵��������ǣ� ��
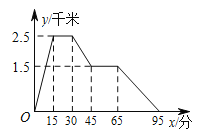
A. ����������ǿ��2.5ǧ�� B. ��ǿ��������������15����
C. ����������͵�4ǧ�� D. ��ǿ����͵�ؼҵ�ƽ���ٶ���3ǧ��/Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ����֪��1+��2=180�㣬��2=��B����˵����DEC+��C=180�㣬�����������գ�

֤��:�ߡ�1+��2=180��(��֪)
��_____��_____(____________________)
��______=��EFC(____________________)
�֡�2=��B(��֪)
���2=______(��������)
��___________(�ڴ������,��ֱ��ƽ��)
���DEC+��C=180��(��ֱ��ƽ��,ͬ���ڽǻ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ӳа���һ�ҹ�˾���ͻ����ҵ��һ������18�֣�����1������5��С�������ڶ�������38�֣�����2������11��С���������������ɵij����պ�װ����
(1)���ֳ��͵����������Ƕ��ٶ֣�
(2)��������һ�εķ���Ϊ200Ԫ��С��������һ�εķ���Ϊ60Ԫ���ڵ�һ�����������������Ŵ�С����,����ʹ��������?(ֱ��д���ɳ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����˸��߳�Ϊ1��С�����ΰڷ���ƽ��ֱ������ϵ�У�����ԭ���ֱ��l��ͼ�ηֳ������ȵ������֣���ֱ��l����ƽ��3����λ������ֱ��l��ĺ�����ϵʽΪ �� 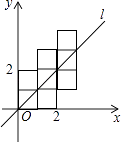
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��m����A��4��0����B��3����![]() ����ֱ��n����ԭ������ֱ��m�ཻ��D��D��ĺ�����Ϊ��2��
����ֱ��n����ԭ������ֱ��m�ཻ��D��D��ĺ�����Ϊ��2��
��1����ֱ��m��n�ı���ʽ��
��2�����OBD�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com