练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE，BC的延长线交DE于F，连接BD，若BC＝2EF，试证明△BED是等腰三角形．

    【答案】见解析

    【解析】

    根据直角三角形的两锐角互余，以及对顶角相等，旋转的性质，即可证得是的垂直平分线，据此即可证得.

    证明：∵将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE，

    ∴DE＝BC，∠ADF＝∠ABC，

    ∵BC＝2EF，

    ∴DF＝EF，

    ∴DE＝2EF，

    ∵在直角△ABC中，∠ABC+∠ACB＝90°，

    又∵∠ABC＝∠ADE，

    ∴∠ACB+∠ADE＝90°．

    ∵∠FCD＝∠ACB，

    ∴∠FCD+∠ADE＝90°，

    ∴∠CFD＝90°，

    ∴BF⊥DE，

    ∵EF＝FD，

    ∴BF垂直平分DE，

    ∴BD＝BE，

    ∴△BDE是等腰三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有一个运输队承包了一家公司运送货物的业务，第一次运送18吨，派了1辆大卡车和5辆小卡车；第二次运送38吨，派了2辆大卡车和11辆小卡车，并且两次派的车都刚好装满。

    (1)两种车型的载重量各是多少吨？

    (2)若大卡车运送一次的费用为200元，小卡车运送一次的费用为60元，在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

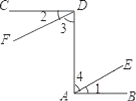
    【题目】已知：如图，CD⊥DA，DA⊥AB，∠1=∠2．试确定射线DF与AE的位置关系，并说明你的理由．

    某同学在解决上面问题时，准备三步走，请你完成他的步骤．

    (1)问题的结论：DF____AE．

    (2)思路要使DF_____AE，只要∠3=____．

    (3)说理过程：

    解：∵CD⊥DA，DA⊥AB，

    ∴∠CDA=∠DAB=________．( )

    又∵∠1=∠2，

    ∴∠CDA﹣∠2=____﹣____，( )

    即∠3=______，

    ∴DF_____AE．( )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线m经过A（4，0）、B（3，﹣），直线n经过原点且与直线m相交于D，D点的横坐标为﹣2．

    （1）求直线m、n的表达式；

    （2）求△OBD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正五边形ABCDE中．

    （1）AC与BE相交于P，求证：四边形PEDC为菱形；
    （2）延长DC、AE交于M点，连BM交CE于N，求证：CN=EP；
    （3）若正五边形边长为2，直接写出AD的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（ ）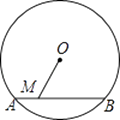
    A.3≤OM≤5
    B.4≤OM≤5
    C.3＜OM＜5
    D.4＜OM＜5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

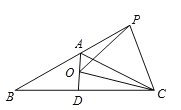
    【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：

    ①∠APO+∠DCO=30°；②△OPC是等边三角形：③AC=DO+AP；④S△ABC=S四形形AOCP．

    其中正确的是_______．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

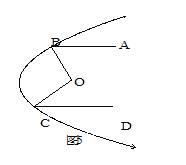
    【题目】问题探究：

    如下面四个图形中， AB∥CD．

    （1）分别说出图1、图2、图3、图4中，∠1与∠2、∠3三者之间的关系．

    （2）请你从中任选一个加以说明理由．

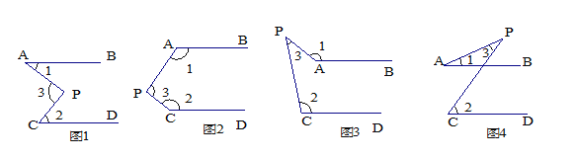
    解决问题：

    （3）如图5所示的是一探照灯灯碗的纵剖面，从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出．如果∠ABO=57°，∠DCO=44°，那么∠BOC=_______°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．

    （1）求证：△AEC≌△ADB；
    （2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．

    查看答案和解析>>

    同步练习册答案