
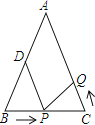
【题目】如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
(1)若点P的速度为3cm/s,用含t的式子表示第t秒时,BP= cm,CP= cm.
(2)在(1)的条件下,若点Q运动速度与点P的运动速度相等,经过几秒钟△BPD与△CQP全等,说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,且点P的速度比点Q的速度慢1cm/s时,点Q的运动速度为多少时?能够使△BPD与△CQP全等?
【答案】(1)3t,8﹣3t;(2)经过1秒钟△BPD与△CQP全等,见解析;(3)Q的速度是5cm/s时,△BPD≌△CQP
【解析】
(1)根据路程=速度×时间就可以得出结论;
(2)当BP=PC时,BD=CQ,由BP+CP=BC=8,得出BP=4,t=![]() s CQ=4不成立;
s CQ=4不成立;
当BP=CQ时,BD=CP,由中点的定义得出BD=AD=5,CP=5,BP=3,即可得出结果;
(3)设Q的速度为acm/s,则P的速度为(a﹣1)cm/s,由BP与CQ不相等,得出BD=CQ,BP=CP,设运动时间为ts,则at=5,(a﹣1)t=4,解得t=1s,a=5cm/s即可.
解:(1)∵由题意得:BP=3t,
∴PC=8﹣3t;
故答案为:3t,8﹣3t;
(2)经过1秒钟△BPD与△CQP全等,理由如下:
当BP=PC时,BD=CQ,
∵BP+CP=BC=8,
∴BP=4,
∴t=![]() s CQ=4不成立;
s CQ=4不成立;
当BP=CQ时,BD=CP,
∵点D为AB的中点,
∴BD=AD,
∵AB=10,
∴BD=5,
∴CP=5,
∴BP=3,
∴t=1,故t=1;
即若点Q运动速度与点P的运动速度相等,经过1秒钟△BPD与△CQP全等;
(3)设Q的速度为acm/s,则P的速度为(a﹣1)cm/s,
∵BP与CQ不相等,
∴BD=CQ,BP=CP,
设运动时间为ts,
∴at=5,(a﹣1)t=4,
∴t=1s,a=5cm/s;
即Q的速度是5cm/s时,△BPD≌△CQP.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】已知A、B两地相距10千米,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A 地距离y(千米)与甲所用的时间x(分)之间的关系如图所示。

(1)甲的速度是 千米/分。
(2)乙的速度是 千米/分,乙到达A地的时间是 。
(3)甲、乙两人相距4千米的时间是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
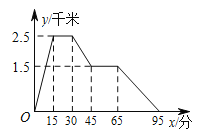
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个运输队承包了一家公司运送货物的业务,第一次运送18吨,派了1辆大卡车和5辆小卡车;第二次运送38吨,派了2辆大卡车和11辆小卡车,并且两次派的车都刚好装满。
(1)两种车型的载重量各是多少吨?
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 . 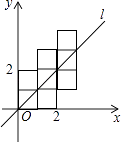
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
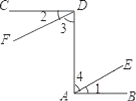
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.
某同学在解决上面问题时,准备三步走,请你完成他的步骤.
(1)问题的结论:DF____AE.
(2)思路要使DF_____AE,只要∠3=____.
(3)说理过程:
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=∠DAB=________.( )
又∵∠1=∠2,
∴∠CDA﹣∠2=____﹣____,( )
即∠3=______,
∴DF_____AE.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
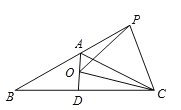
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:
①∠APO+∠DCO=30°;②△OPC是等边三角形:③AC=DO+AP;④S△ABC=S四形形AOCP.
其中正确的是_______.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com