
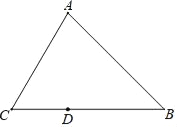
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.
【答案】(1)见解析;(2)结论:DE=2BF.理由见解析.
【解析】
(1)根据题意画出图形即可;
(2)结论:DE=2BF.连接AD,设DE交AC于H.想办法证明△ADH≌△DBF即可解决问题;
解:(1)依题意补全图形如图所示:
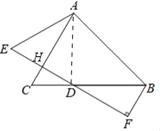
(2)结论:DE=2BF.
理由:连接AD,设DE交AC于H.
∵点E、D关于AC对称,
∴AC垂直平分DE.
∴AE=AD.
∵AE=BD,∴AD=DB.
∴∠DAB=∠ABC=45°.
∴∠ADC=90°.
∴∠ADE+∠BDF=90°.
∵BF⊥ED,AC⊥ED,
∴∠F=∠AHD=90°.
∴∠DBF+∠BDF=90°.
∴∠DBF=∠ADH.
∴△ADH≌△DBF
∴DH=BF
又∵DH=EH,
∴DE=2BF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x与反比例函数y=![]() (x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(1)求点A的坐标;
(2)若四边形ABOC的面积为3,求一次函数y=kx+b的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一电子白板和一批笔记本电脑,经投标,购买一块电子白板比买三台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买一块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况需购买电子白板和笔记本电脑的总数为396台,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )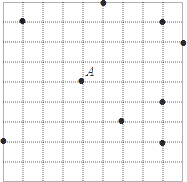
A.2 ![]() <r<
<r< ![]()
B.![]() <r≤3
<r≤3 ![]()
C.![]() <r<5
<r<5
D.5<r< ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 . 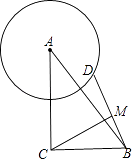
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边中点,点E是BC边上一点,将△ADE沿DE折叠,得到△FDE,使△FDE与△BDE重叠部分的面积是△AEB面积的![]() ,若AC=3,BC=6,则线段BE的长为__________.
,若AC=3,BC=6,则线段BE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com