
����Ŀ����������С��һ�ҹ�7�˴�ij�س���ȥ�ι������ᣮС�����飺�ðְ�����үү�����̡��������ȥ���Լ��������ij41·��ȥ������ڵ���8����ij����ݻ�ϣ�ͼ��![]() �ֱ��ʾij41·����С�γ�����ʻ�е�·�̣�ǧ�ף���ʱ�䣨���ӣ���ϵ���Թ۲�ͼ�ش��������⣺
�ֱ��ʾij41·����С�γ�����ʻ�е�·�̣�ǧ�ף���ʱ�䣨���ӣ���ϵ���Թ۲�ͼ�ش��������⣺

��1��ij41·����;����ʻ��ƽ���ٶ�Ϊ ǧ��/���ӣ��˴���ʻ��·���� ǧ�ף�
��2��д��С�γ�����ʻ������![]() ��
��![]() �ĺ�����ϵʽ�� ��������Ϊ ��
�ĺ�����ϵʽ�� ��������Ϊ ��
��3��С�������������ij41·���� ���Ӻְֵ�С�γ�����.
���𰸡���1��![]() ��40��2��S=
��40��2��S=![]() t-
t-![]() ; 5��t��41��3��25
; 5��t��41��3��25
��������
��1������ͼ�����ݿ�֪![]() ��ʾ41·����·�̺����ݹ�ϵͼ������ͼ�����ݼ��ɽ��
��ʾ41·����·�̺����ݹ�ϵͼ������ͼ�����ݼ��ɽ��
��2��![]() ��ʾС�γ���·����ʱ��Ĺ�ϵ����֪�㣨5��0���ͣ�41��40��,�����ϵʽΪS=kt+b,����֪����뼴�ɽ��
��ʾС�γ���·����ʱ��Ĺ�ϵ����֪�㣨5��0���ͣ�41��40��,�����ϵʽΪS=kt+b,����֪����뼴�ɽ��
��3���ۺ���������⣬�г�С�γ���41·���Ľ���ʽ������⼴��
��1��ƽ���ٶ�=![]() =
=![]() ��ǧ��/���ӣ�
��ǧ��/���ӣ�
·����40ǧ��
��2����ͼ���֪![]() ����������֪�㣨5��0���ͣ�41��40��
����������֪�㣨5��0���ͣ�41��40��
��С�γ�����ʻ������![]() ��
��![]() �ĺ�����ϵʽΪ��S=kt+b
�ĺ�����ϵʽΪ��S=kt+b
�ѣ�5��0���ͣ�41��40���������ʽ��![]()
���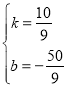
��S=![]() t-
t-![]()
��ͼ��֪�䶨����Ϊ��5��t��41��
��3����41·������ʻ������![]() ��
��![]() �ĺ�����ϵʽΪ��S=k
�ĺ�����ϵʽΪ��S=k![]() t+b
t+b
�ѣ�45��40����0��0������![]()
���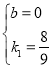
��41·���Ľ���ʽΪS=![]()
�ۺϿɵ�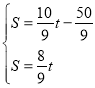
���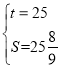
���ڳ���25���ӵ�ʱ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����κ���y��ax2��bx��c(a ![]() 0)��ͼ��������4�����ۣ���abc>0����b>a��c����4a��2b��c>0����b2��4ac>0��������ȷ���� ��
0)��ͼ��������4�����ۣ���abc>0����b>a��c����4a��2b��c>0����b2��4ac>0��������ȷ���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ѧУ֮����һ����ֱ�Ĺ�·���緹��С������ǰ��ѧУ��;�з����������壬ͣ�¸������绰������ӵ��绰���ϻ������ϸ���ѧУ��ͬʱС����ԭ·���أ�����������С����������ѧУ��������ԭ·����16min���ң��ٹ�5minС������ѧУ��С��ʼ����100m/min���ٶȲ��У�С��������ľ���y����λ��m����С������绰��IJ���ʱ��t����λ��min��֮��ĺ�����ϵ��ͼ��ʾ����������˵����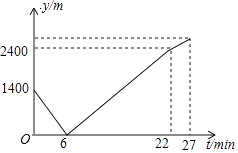
�ٴ�绰ʱ��С��������ľ���Ϊ1400�ף�
��С������������������ؼ��ٶ�Ϊ50m/min��
��С������绰����27min����ѧУ��
��С������ѧУ�ľ���Ϊ2900m��
������ȷ�ĸ����ǣ� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1��1��1����ֱ��y=x�ϣ�����A1�ֱ���y�ᡢx���ƽ���߽�ֱ��y= ![]() x�ڵ�B1 �� B2 �� ����B2��y���ƽ���߽�ֱ��y=x�ڵ�A2 �� ����A2��x���ƽ���߽�ֱ��y=
x�ڵ�B1 �� B2 �� ����B2��y���ƽ���߽�ֱ��y=x�ڵ�A2 �� ����A2��x���ƽ���߽�ֱ��y= ![]() x�ڵ�B3 �� �������մ˹��ɽ�����ȥ�����An�ĺ�����Ϊ ��
x�ڵ�B3 �� �������մ˹��ɽ�����ȥ�����An�ĺ�����Ϊ �� 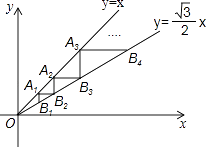
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
��ƽ��ֱ������ϵxOy�У���P��x0 �� y0����ֱ��Ax+By+C=0�ľ��빫ʽΪ��d= ![]() ��
��
���磺���P0��0��0����ֱ��4x+3y��3=0�ľ��룮
�⣺��ֱ��4x+3y��3=0֪��A=4��B=3��C=��3��
���P0��0��0����ֱ��4x+3y��3=0�ľ���Ϊd= ![]() =
= ![]() ��
��
�������ϲ��ϣ�����������⣺
��1����P1��3��4����ֱ��y=�� ![]() x+
x+ ![]() �ľ���Ϊ��
�ľ���Ϊ��
��2����֪����C���Ե�C��2��1��ΪԲ�ģ�1Ϊ�뾶��Բ����C��ֱ��y=�� ![]() x+b���У���ʵ��b��ֵ��
x+b���У���ʵ��b��ֵ��
��3����ͼ�����PΪ����2�С�C�ϵ�����һ�㣬��A��BΪֱ��3x+4y+5=0�ϵ����㣬��AB=2�������S��ABP�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܳ���ȵ��������Ρ����ı��Ρ��������ε����S3��S4��S6��Ĵ�С��ϵ�ǣ� ��
A.S3��S4��S6
B.S6��S4��S3
C.S6��S3��S4
D.S4��S6��S3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ�����ʦ˵����![]() ������������������������ѭ��С����ͬѧ�ǣ����ܰ�
������������������������ѭ��С����ͬѧ�ǣ����ܰ�![]() ��С������ȫ��д��������������۷ף�����ͬѧ˵����Ҫ������С������ȫ��д�����Ƿdz��ѵģ������ǿ�����(
��С������ȫ��д��������������۷ף�����ͬѧ˵����Ҫ������С������ȫ��д�����Ƿdz��ѵģ������ǿ�����(![]() ��1)��ʾ����С�����֣�������ʦ˵��������ͬѧ��˵������ȷ�ģ���Ϊ1��2��4������1��
��1)��ʾ����С�����֣�������ʦ˵��������ͬѧ��˵������ȷ�ģ���Ϊ1��2��4������1��![]() ��2������
��2������![]() ������������1�����������ȥ���������֣������С�����֣�������˵������Ȼ��ˣ���Ϊ2��
������������1�����������ȥ���������֣������С�����֣�������˵������Ȼ��ˣ���Ϊ2��![]() ��3������
��3������![]() ��С�����־���(
��С�����־���(![]() ��2)�ˣ�������ʦ˵����������ĺܴ����������ţ�����ʦ��ʾ��һ����ϰ�⣺����֪8+
��2)�ˣ�������ʦ˵����������ĺܴ����������ţ�����ʦ��ʾ��һ����ϰ�⣺����֪8+![]() =x+y������x��һ����������0��y��1���������2x+(
=x+y������x��һ����������0��y��1���������2x+(![]() ��y)2019��ֵ������ͬ���������������ȷ�𰸣�
��y)2019��ֵ������ͬ���������������ȷ�𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����2x+4��x�ᡢy��ֱ���A��B���㣬P��ֱ��AB�ϵ�һ�����㣬��C������Ϊ����4��0����PC��y�����D��O��ԭ�㣮
��1�����AOB�������
��2���߶�AB�ϴ���һ��P��ʹ��DOC�ա�AOB�����ʱ��P�����ꣻ
��3��ֱ��AB�ϴ���һ��P��ʹ��P��C��OΪ�����������������AOB�����ȣ����P������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ�ƴ����ͼ��ʾ��ͼ�Σ�����C��CFƽ����DCE��DE�ڵ�F��

��1����֤��CF��AB��
��2������DFC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com