
【题目】如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= ![]() x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y=
x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= ![]() x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .
x于点B3 , …,按照此规律进行下去,则点An的横坐标为 . 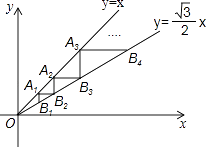
【答案】![]()
【解析】解:∵AnBn+1∥x轴,
∴tan∠AnBn+1Bn= ![]() .
.
当x=1时,y= ![]() x=
x= ![]() ,
,
∴点B1的坐标为(1, ![]() ),
),
∴A1B1=1﹣ ![]() ,A1B2=
,A1B2= ![]() =
= ![]() ﹣1.
﹣1.
∵1+A1B2= ![]() ,
,
∴点A2的坐标为( ![]() ,
, ![]() ),点B2的坐标为(
),点B2的坐标为( ![]() ,1),
,1),
∴A2B2= ![]() ﹣1,A2B3=
﹣1,A2B3= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴点A3的坐标为( ![]() ,
, ![]() ),点B3的坐标为(
),点B3的坐标为( ![]() ,
, ![]() ).
).
同理,可得:点An的坐标为( ![]() ,
, ![]() ).
).
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠B、∠D的两边分别平行.
(1)在图1中, ∠B与∠D的数量关系是 ;
(2)在图2中, ∠B与∠D的数量关系是 ;
(3)用一句话归纳的结论为
(4)应用:若两个角的两边分别互相平行,其中一个角比另一个角的2倍小30°,求着两个角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d= ![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= ![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上周六,小明一家共7人从某地出发去参观世博会.小明提议:让爸爸载着爷爷、奶奶、外公、外婆去,自己和妈妈从某41路车去,最后在地铁8号线某博物馆汇合,图中![]() 分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:

(1)某41路车在途中行驶的平均速度为 千米/分钟;此次行驶的路程是 千米;
(2)写出小轿车在行驶过程中![]() 与
与![]() 的函数关系式: ,定义域为 ;
的函数关系式: ,定义域为 ;
(3)小明和妈妈乘坐的某41路出发 分钟后被爸爸的小轿车追上了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=![]() 计算.解答下列问题:
计算.解答下列问题:

(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
(3)已知点A(5,5),B(-4,7),点P在x轴上,且要使PA+PB的和最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )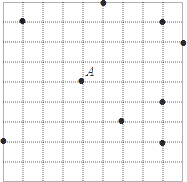
A.2 ![]() <r<
<r< ![]()
B.![]() <r≤3
<r≤3 ![]()
C.![]() <r<5
<r<5
D.5<r< ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com