
【题目】如图,两个以点O为圆心的同心圆,
图1 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
【答案】
(1)解:AC=BD,理由是:
过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,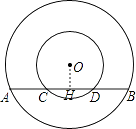
AH-CH=BH-DH,
即AC=BD
(2)解:连接OC,如图,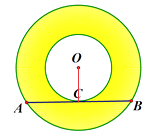
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)解:如图,连接OB.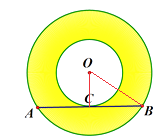
∵大圆的弦AB是小圆的切线, ∴OC⊥AB,AC=CB, ∴OB2-OC2=(20÷2)2=102 , ∵S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2), ∴S圆环=100πcm2
【解析】(1)AC=BD,理由是:过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,根据等式的性质得出AH-CH=BH-DH,从而得出AC=BD ;
(2)连接OC,如图,根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ;
(3)连接OB.根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ,然后根据勾股定理及等式的性质得出OB2-OC2=(20÷2)2=102 ,然后根据S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2)算出答案。


科目:初中数学 来源: 题型:
【题目】如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )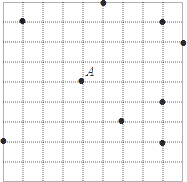
A.2 ![]() <r<
<r< ![]()
B.![]() <r≤3
<r≤3 ![]()
C.![]() <r<5
<r<5
D.5<r< ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴华商店准备购进甲、乙两种书包出售,每个甲种书包的进价比每个乙种书包的进价多20元,购进3个甲种书包的费用和购进4个乙种书包的费用相等,现计划购进两种书包共100个,其中乙种书包不少于35个.
(1)甲种书包进价为__________元/个,乙种书包进价为__________元/个;
(2)若甲种书包每个售价120元,乙种书包每个售价90元,且购进这100个书包的费用不低于7200元,如果这100个书包都可售完,那么兴华商店如何进货才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
已知:如图,四边形ABCD是平行四边形;
求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(1)连接AC;
(2)作AC的垂直平分线EF分别交BC,AD于E,F.
(3)连接AE,CF
所以四边形AECF是菱形.
老师说:“小凯的作法正确”.
回答问题:
已知:在平行四边形ABCD中,点E、F分别在边BC、AD上______________________________________________.(补全已知条件)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com