
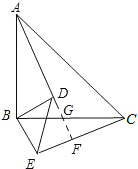
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由等腰直角三角形的性质得出AB=BC,BD=BE,∠ABC=∠DBE=90°,得出∠ABD=CBE,证出△ABD≌△CBE(SAS),得出AD=CE;
(2)△ABD≌△CBE得出∠BAD=∠BCE,再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,得出∠AFC=∠ABC=90°,证出结论.
(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=CBE,
在△ABD和△CBE中,
 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE;
(2)延长AD分别交BC和CE于G和F,如图所示:
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.


科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数![]() ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
分数(单位:分) | 105 | 130 | 140 | 150 |
人数(单位:人) | 2 | 4 | 3 | 1 |
下列说法中,不正确的是( )
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生参加交通安全知识网络测试活动.小王对九年(3)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整), 
请你根据图中所给的信息解答下列问题:
(1)九年(3)班有名学生,并把折线统计图补充完整;
(2)已知该市共有12000名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
(3)小王查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有5400人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因;
(4)该班从成绩前3名(2男1女)的学生中随机抽取2名参加复赛,请用树状图或列表法求出抽到“一男一女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E. 
(1)求证:EF是⊙O的切线;
(2)当BD=3,DF= ![]() 时,求直径AB.
时,求直径AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.
①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com