
【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP= ![]() ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=![]() 计算.解答下列问题:
计算.解答下列问题:

(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
(3)已知点A(5,5),B(-4,7),点P在x轴上,且要使PA+PB的和最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )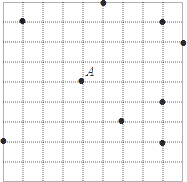
A.2 ![]() <r<
<r< ![]()
B.![]() <r≤3
<r≤3 ![]()
C.![]() <r<5
<r<5
D.5<r< ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
A. ∠E=∠FB. ∠E+∠F=180°
C. 3∠E+∠F=360°D. 2∠E-∠F=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com