
【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
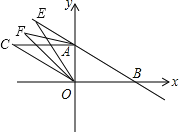
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

【答案】(1)A(0,3),B(4,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据非负数的性质列式求出m、n的值,然后写出点A、B的坐标即可;
(2)设点E的横坐标为a,然后利用三角形的面积列式求出a的值,再利用待定系数法求出直线AB的解析式,然后求解即可;
(3)根据平移的性质可得AB∥OC,AC∥OB,根据平行线的性质可得∠OEB=∠COE,∠CAE=∠ABO,然后根据角平分线的定义可得![]() ,
,![]() ,再根据三角形的内角和定理列式整理即可得解.
,再根据三角形的内角和定理列式整理即可得解.
解:(1)由非负数的性质得,m-3=0,n-4=0,
解得m=3,n=4,
所以,A(0,3)B(4,0);
(2)设点E的横坐标为a,
![]() ,
,
![]() ,
,
解得a=![]() ,
,
设直线AB的解析式为y=kx+b,
则![]()
解得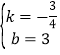
所以,直线AB的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
所以,点E的坐标为![]() ;
;
(3)由平移的性质,AB∥OC,AC∥OB,
∴∠OEB=∠COE,∠CAE=∠ABO,
∵OF平分∠COE,AF平分∠EAC,
![]() ,
,
由三角形的内角和定理,∠OEB+∠EAF=∠F+∠EOF,
![]() ,
,
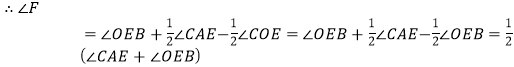 ,
,
∵∠ABO+∠OEB=α,
![]() .
.


科目:初中数学 来源: 题型:
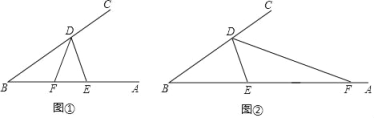
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0)…… 根据这个规律探索可得,第50个点的坐标为( )
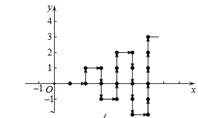
A. (10,-5)B. (10,-1) C. (10,0) D. (10,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
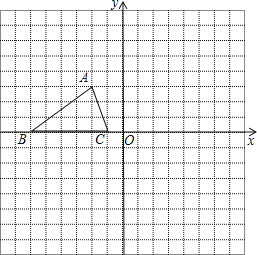
(1)请直接写出点A关于y轴对称的点的坐标为 ;
(2)将△ABC平移,使点B移动后的坐标为B′(﹣5,﹣5),画出平移后的图形△A′B′C′;
(3)将△ABC绕坐标原点O顺时针旋转90°,画出旋转后的图形△A″B″C″.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP= ![]() ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C,(﹣1,﹣2),D(1,﹣2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2019次相遇时的坐标为_____.
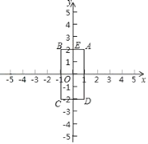
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解: ∵EF∥AD,
∴∠2=____(____________________________)
又∵∠1=∠2
∴∠1=∠3(等量代换)
∵AB∥_____(_____________________________)
∴∠BAC+______=180°(___________________________)
∵∠BAC=70°
∴∠AGD=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com