
【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积.
【答案】
(1)解:用尺规作三角形的内切圆如图:
(2)解:∵等边三角形的周长为36米,
∴等边三角形的边长为12米, tan∠OBD= ![]() ,
,
∵∠OBD=30°,BD=6,
∴ ![]() ∴DO=2
∴DO=2 ![]() ,
,
∴内切圆半径为2 ![]() m2 ,
m2 ,
则花坛面积为:πr2=12πm2 .
【解析】 (1)分别作出∠ABC与∠ACB的角平分线,两线相交于点O,过点O作OD⊥BC于点D,然后以点O为圆心,OD为半径画圆,此圆就是所求得圆形花坛;
(2)根据等边三角形的周长算出其边长,根据正切三角函数的定义及特殊锐角的三角函数值得出方程,求解得出圆的半径,根据圆的面积公式计算出圆形花坛的面积 。
【考点精析】通过灵活运用三角形的内切圆与内心和锐角三角函数的定义,掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别相交于A、B两点,与直线
与x轴、y轴分别相交于A、B两点,与直线![]() 交于点C,且点C的横坐标为1.
交于点C,且点C的横坐标为1.
(1)求b的值;
(2)点![]() ,
,![]() 在直线
在直线![]() 上,若
上,若![]() ,则
,则![]() __________
__________![]() .
.
(3)若动点P在线段OC上(点P不与点C重合),连接PA,PB,设点P的横坐标为m,△PAB的面积为S,求S关于m的函数关系式(不要求写出自变量m的取值范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
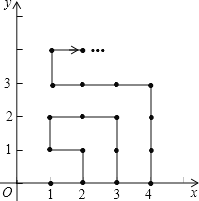
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com