
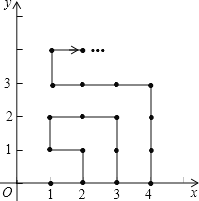
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
【答案】![]()
【解析】
根据点的坐标的变化可得出“第(2n1)2个点的坐标为(2n1,0)(n为正整数)”,依此规律可得出第2025个点的坐标为(45,0),再结合第2019个点在第2025个点的上方6个单位长度处,即可求出第2019个点的坐标,此题得解.
解:观察图形,可知:第1个点的坐标为(1,0),第4个点的坐标为(1,1),第9个点的坐标为(3,0),第16个点的坐标为(1,3),…,
∴第(2n1)2个点的坐标为(2n1,0)(n为正整数).
∵2025=452,
∴第2025个点的坐标为(45,0).
又∵20256=2019,
∴第2019个点在第2025个点的上方6个单位长度处,
∴第2019个点的坐标为(45,6).
故答案为:(45,6).


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x﹣1=0,②![]() x+1=0,③x﹣(3x+1)=﹣5中,不等式组
x+1=0,③x﹣(3x+1)=﹣5中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组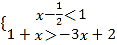 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程3﹣x=2x,3+x=2(x+![]() )都是关于x的不等式组
)都是关于x的不等式组![]() 的关联方程,直接写出m的取值范围.
的关联方程,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=![]() ,
,![]() ;
;
OA32=12+![]() ,
,![]() ;
;
OA42=12+![]() ,
,![]() …
…
(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2等于多少;Sn等于多少.
(2)求出OA10的长.
(3)若一个三角形的面积是![]() ,计算说明他是第几个三角形?
,计算说明他是第几个三角形?
(4)求出S12+S22+S32+…+S102的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?(结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
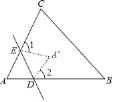
【题目】如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示玲玲骑自行车离家的距离与时间的关系.她9点离开家,15点回到家,请根据图象回答下列问题:

(1)玲玲到达离家最远的地方是什么时间?她离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)第一次休息时,她离家多远?
(4)11点~12点她骑车前进了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com