
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
【答案】(1)![]() ;(2)有三种购车方案,方案一:购买A型公交车6辆,购买B型公交车4辆;方案二:购买A型公交车7辆,购买B型公交车3辆;方案三:购买A型公交车8辆,购买B型公交车2辆;(3)总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.
;(2)有三种购车方案,方案一:购买A型公交车6辆,购买B型公交车4辆;方案二:购买A型公交车7辆,购买B型公交车3辆;方案三:购买A型公交车8辆,购买B型公交车2辆;(3)总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.
【解析】
(1)根据“购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元”列出二元一次方程组求解可得;
(2)购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,根据“总费用不超过1200万元、年载客量总和不少于680万人次”列一元一次不等式组求解可得;
(3)设购车总费用为w万元,根据总费用的数量关系得出w=100m+150(10﹣m)=﹣50m+1500,再进一步利用一次函数的性质求解可得.
(1)由题意,得![]() ,
,
解得![]() ;
;
(2)设购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,
由题意,得![]() ,
,
解得6≤m≤8,
∵m为整数,
∴有三种购车方案
方案一:购买A型公交车6辆,购买B型公交车4辆;
方案二:购买A型公交车7辆,购买B型公交车3辆;
方案三:购买A型公交车8辆,购买B型公交车2辆.
(3)设购车总费用为w万元
则w=100m+150(10﹣m)=﹣50m+1500,
∵﹣50<0,6≤m≤8且m为整数,
∴m=8时,w最小=1100,
∴购车总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
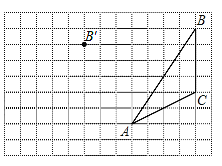
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为 1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)线段 AA′与线段 BB′的数量和位置关系是___________;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250( ![]() +1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.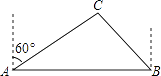
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣ ![]() x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).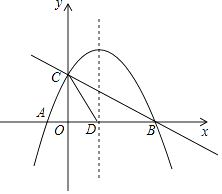
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上:是否存在一点M,使|MA﹣MC|的值最大;是否存在一点N,使△NCD是以CD为腰的等腰三角形?若存在,直接写出点M,点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
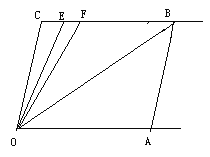
【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若﹣ ![]() a≥b,则a≤﹣2b,其根据是( )
a≥b,则a≤﹣2b,其根据是( )
A.不等式的两边都加上(或减去)同一个整式,不等号的方向不变
B.不等式的两边都乘(或除以)同一个正数,不等号的方向不变
C.不等式的两边都乘(或除以)同一个负数,不等号的方向改变
D.以上答案均不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com