
【题目】如图,直线y1=﹣ ![]() x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).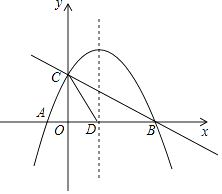
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上:是否存在一点M,使|MA﹣MC|的值最大;是否存在一点N,使△NCD是以CD为腰的等腰三角形?若存在,直接写出点M,点N的坐标;若不存在,请说明理由.
【答案】
(1)解:令x=0,可得y=2,令y=0,可得x=4,即点B(4,0),C(0,2);
设二次函数的解析式为y=ax2+bx+c,将点A、B、C的坐标代入解析式得,
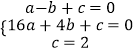 ,解得:
,解得: 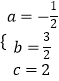 ,
,
∴二次函数的关系式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)解:如图1,过点P作PN⊥x轴于点N,交BC于点M,过点C作CE⊥PN于E,
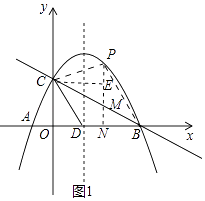
设M(a,﹣ ![]() a+2),P(a,﹣
a+2),P(a,﹣ ![]() a2+
a2+ ![]() a+2),
a+2),
∴PM=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() a+2)=﹣
a+2)=﹣ ![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴点D的坐标为:( ![]() ,0),
,0),
∵S四边形PCDB=S△BCD+S△CPM+S△PMB= ![]() BDOC+
BDOC+ ![]() PMCE+
PMCE+ ![]() PMBN,
PMBN,
= ![]() +
+ ![]() a(﹣
a(﹣ ![]() a2+2a)+
a2+2a)+ ![]() (4﹣a)(﹣
(4﹣a)(﹣ ![]() a2+2a),
a2+2a),
=﹣a2+4a+ ![]() (0≤x≤4).
(0≤x≤4).
=﹣(a﹣2)2+ ![]() ,
,
∴a=2时,S四边形PCDB的面积最大= ![]() ,
,
∴﹣ ![]() a2+
a2+ ![]() a+2=﹣
a+2=﹣ ![]() ×22+
×22+ ![]() ×2+2=3,
×2+2=3,
∴点P坐标为:(2,3),
∴当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为 ![]()
(3)解:如图2中,
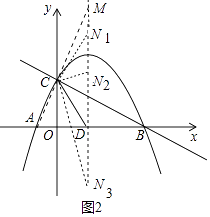
∵A(﹣1,0),C(0,2),
∴直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,
∴M( ![]() ,5).
,5).
∵抛物线的对称轴是x= ![]() ,
,
∴OD= ![]() ,
,
∵C(0,2),
∴OC=2.在Rt△OCD中,由勾股定理,得CD= ![]() =
= ![]() ,
,
∵△CDN是以CD为腰的等腰三角形,
∴CN1=DN2=DN3=CD.
如图2所示,作CE⊥对称轴于E,
∴EN1=ED=2,
∴DN1=4.
∴N1( ![]() ,4),N2(
,4),N2( ![]() ,
, ![]() ),N3(
),N3( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)根据x轴上点的坐标是(x,0),y轴点的坐标是(0,y),直线y1=﹣![]() x+2与x轴,y轴分别交于B,C,得到点B(4,0)、C(0,2),由抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0),用待定系数法求出抛物线的解析式;(2)由抛物线的对称轴与x轴交于点D,得到点D的坐标(
x+2与x轴,y轴分别交于B,C,得到点B(4,0)、C(0,2),由抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0),用待定系数法求出抛物线的解析式;(2)由抛物线的对称轴与x轴交于点D,得到点D的坐标( ![]() ,0),由S四边形PCDB=S△BCD+S△CPM+S△PMB ,得到点P坐标(2,3),所以当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为
,0),由S四边形PCDB=S△BCD+S△CPM+S△PMB ,得到点P坐标(2,3),所以当点P运动到(2,3)时,四边形PCDB的面积最大,最大值为 ![]() ;(3)由A(﹣1,0),C(0,2),代入得到直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,得到M(
;(3)由A(﹣1,0),C(0,2),代入得到直线AC的解析式为y=2x+2,直线AC与对称轴的交点即为点M,此时|MA﹣MC|的值最大,得到M(![]() ,5),抛物线的对称轴是x=
,5),抛物线的对称轴是x=![]() ,得到OD=
,得到OD= ![]() ,由C(0,2),得到OC=2;在Rt△OCD中,由勾股定理,得CD=
,由C(0,2),得到OC=2;在Rt△OCD中,由勾股定理,得CD=![]() ,由△CDN是以CD为腰的等腰三角形,得到CN1=DN2=DN3=CD,如图2所示,作CE⊥对称轴于E,得到EN1=ED=2,DN1=4,所以N1(
,由△CDN是以CD为腰的等腰三角形,得到CN1=DN2=DN3=CD,如图2所示,作CE⊥对称轴于E,得到EN1=ED=2,DN1=4,所以N1(![]() ,4),N2(
,4),N2(![]() ,
,![]() ),N3(
),N3( ![]() ,﹣
,﹣![]() );此题是综合题,难度较大,计算和解方程时需认真仔细.
);此题是综合题,难度较大,计算和解方程时需认真仔细.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
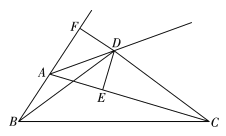
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧 ![]() 的长为 .
的长为 . 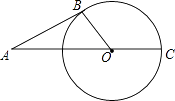
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
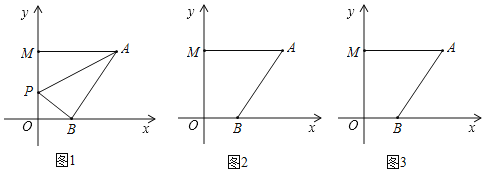
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣荣是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2、4、6、8,…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
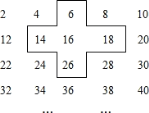
![]() 十字框中的五个数的和与中间的数16有什么关系?
十字框中的五个数的和与中间的数16有什么关系?
![]() 设中间的数为x,用代数式表示十字框中的五个数的和;
设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其中五个数的和能等于2018吗?如能,写出这五个数,如不能,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com