
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
【答案】(1)有三种组建方案:方案一,中型图书角18个,小型图书角12个;方案二,中型图书角19个,小型图书角11个;方案三,中型图书角20个,小型图书角10个;
(2)方案一费用最低,最低费用是22320元.
【解析】
(1)设组建中型图书角x个,则组建小型图书角为(30-x)个;根据不等关系:①科技类书籍不超过1900本;②人文类书籍不超过1620本.列不等式组,进行求解;
(2)此题有两种方法:方法一:因为总个数是不变的,所以费用少的越多,总费用越少;
方法二:分别计算(1)中方案的价钱,再进一步比较.
解:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.
由题意得![]()
解这个不等式组得18≤x≤20.
由于x只能取整数,
∴x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;当x=20时,30-x=10.
故有三种组建方案:方案一,组建中型图书角18个,小型图书角12个;方案二,组建中型图书角19个,小型图书角11个;方案三,组建中型图书角20个,小型图书角10个.
(2)方法一:由于组建一个中型图书角的费用大于组建一个小型图书角的费用,因此组建中型图书角的数量越少,费用就越低,故方案一费用最低,
最低费用是860×18+570×12=22320(元).
方法二:①方案一的费用是:860×18+570×12=22320(元);
②方案二的费用是:860×19+570×11=22610(元);
③方案三的费用是:860×20+570×10=22900(元)
故方案一费用最低,最低费用是22320元.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
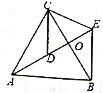
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一条直线上,BC和AE相交于点O,连接BE,若∠CAB=∠CBA=∠CDE=∠CED=50°。
(1)求证:AD=BE;
(2)求∠AEB。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣ ![]() x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).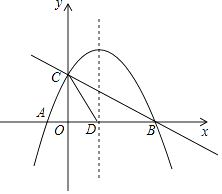
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上:是否存在一点M,使|MA﹣MC|的值最大;是否存在一点N,使△NCD是以CD为腰的等腰三角形?若存在,直接写出点M,点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )
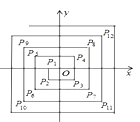
A. (504,504) B. (﹣504,504) C. (﹣504,﹣504) D. (﹣505,504)
查看答案和解析>>
科目:初中数学 来源: 题型:
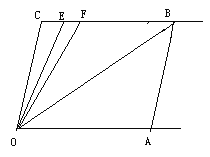
【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清晨,张强从家跑步去迎泽公园,在公园锻炼了一段时间后,又去附近早餐店吃早餐,然后散步走回家.下图反映了这段时间内,张强离家的距离随离家时间的变化而变化的情况,其中![]() (分)表示张强离家时间,
(分)表示张强离家时间,![]() (千米)表示他离家的距离.根据图象所反映的信息,以下四个说法正确的是( )
(千米)表示他离家的距离.根据图象所反映的信息,以下四个说法正确的是( )
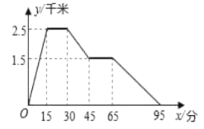
①迎泽公园离张强家2.5千米.
②张强在迎泽公园锻炼了15分钟.
③迎泽公园离早餐店4千米.
④张强从早餐店回家的平均速度是3千米/小时.
A.①②B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
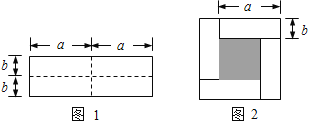
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=33°,则∠K=__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com