
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=33°,则∠K=__________.

【答案】82°
【解析】
分别过K、H作AB的平行线MN和RS,根据平行线的性质和角平分线的性质可用∠ABK和∠DCK分别表示出∠H和∠K,从而可找到∠H和∠K的关系,结合条件可求得∠K.
如图,分别过K、H作AB的平行线MN和RS.
∵AB∥CD,∴AB∥CD∥RS∥MN,∴∠RHB=∠ABE![]() ∠ABK,∠SHC=∠DCF
∠ABK,∠SHC=∠DCF![]() ∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°
∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°![]() (∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC.
(∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC.
又∵∠BKC﹣∠BHC=33°,∴∠BHC=∠BKC﹣33°,∴∠BKC=180°﹣2(∠BKC﹣33°),∴∠BKC=82°.

故答案为:82°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论有( )
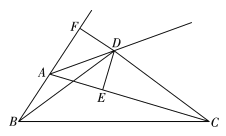
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学胜.
(1)当x=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
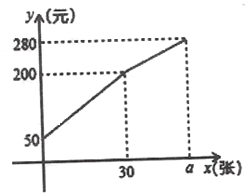
【题目】学校组织义捐义卖活动,小明的小组准备自制贺年卡进行义卖.活动当天,为了方便,小组准备了一些零钱备用,按照定价售出一些贺年卡后,又降价出售,小组所拥有的所有钱数![]() (元)与售出卡片
(元)与售出卡片![]() (张)之间的关系如图所示.
(张)之间的关系如图所示.
(1)求降价前![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)如果按照定价打八折后,将剩余的卡片全部卖出,这时,小组一共有![]() 元钱(含备用领钱),求该小组一共准备了多少张卡片?
元钱(含备用领钱),求该小组一共准备了多少张卡片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )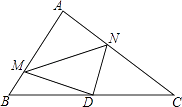
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com