
【题目】如图,一次函数y= ![]() x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。
x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。
(1)求点A、 B的坐标及线段BC的长度;
(2)当点P在什么位置时,△APQ≌△CBP,说明理由;
(3)当△PQB为等腰三角形时,求点P的坐标.

【答案】A(-4,0),B(0,3),BC=5;(1,0);(1,0)或(![]() ,0).
,0).
【解析】
试题根据函数解析式和勾股定理求出点A和点B的坐标以及BC的长度;根据全等的性质得出点P的坐标;本题分PQ=PB,BQ=BP乙BQ=PQ三种情况分别进行计算得出点P的坐标.
试题解析:(1)点A坐标是(-4,0),点B的坐标(0,3),BC=5.
(2)点P在(1,0)时
(3)i)当PQ=PB时,△APQ≌△CBP, 由(1)知此时点P(1,0)
ii)当BQ=BP时,∠BQP=∠BPQ ∠BQP是△APQ的外角,∠BQP>∠BAP,又∠BPQ=∠BAO
∴这种情况不可能
iii)当BQ=PQ时,∠QBP=∠QPB 又∠BPQ=∠BAO,∴∠QBP=∠BAO,则AP=4+x,BP=![]()
∴ 4+x=![]() ,解得x=
,解得x=![]() ,此时点P的坐标为:(
,此时点P的坐标为:(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①若![]() ,则
,则![]() ;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④
;②整数和分数统称为有理数;③绝对值等于它本身的整数是0;④![]() 是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数,其中判断正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]() .
.
(2)如图,一次函数y=x+b与反比例函数![]() 在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO=
在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO= ![]() ,求一次函数和反比例函数的解析式.
,求一次函数和反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
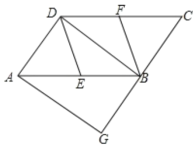
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为充分发挥市场机制和价格杠杆在水资源配置中的作用,促进节约用水,提高用水效率,2017年7月1日起某地实行阶梯水价,价目如右表(注:水费按月结算,m3表示立方米):例:某户居民5月份共用水23m3,则应缴水费3×18+4×(23-18)=74(元).
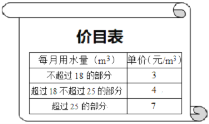
(1)若A居民家1月份共用水12m3,则应缴水费__________元;
(2)若B居民家2月份共缴水费66元,则用水__________m3;
(3)若C居民家3月份用水量为am3(a低于20m3,即a<20),且C居民家3、4两个月用水量共40m3,求3、4两个月共缴水费多少元?(用含a的代数式表示,不要求化简)
(4)在(3)中,当a=19时,求C居民家3、4两个月共缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
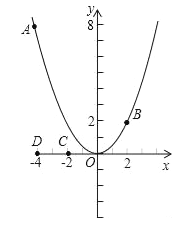
【题目】如图,已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2,记平移后点A的对应点为A′,点B的对应点为B′,点C(﹣2,0)和点D(﹣4,0)是x轴上的两个定点.
①当抛物线向左平移到某个位置时,A′C+CB′最短,求此时抛物线的函数解析式;
②当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
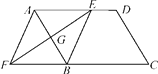
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com