
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.
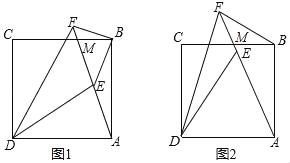
【答案】(1)AB=6;(2)证明见解析.
【解析】
(1)设BM=x,则CM=2x,BC=BA=3x;在Rt△ABM中,E为斜边AM中点,根据直角三角形斜边的中线等于斜边的一半可得AM=2BE=2![]() .由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=
.由勾股定理可得AM2=MB2+AB2,即可得40=x2+9x2,解得x=2.所以AB=3x=6;(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.证明△ABF≌△ADH,根据全等三角形的性质可得AF=AH,BF=DH.再由Rt△FAH是等腰直角三角形,可得HF=![]() AF.由HF=DH+DF=BF+DF,可得BF+DF=
AF.由HF=DH+DF=BF+DF,可得BF+DF=![]() AF.
AF.
解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,
∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2![]() .
.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
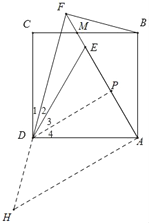
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=![]() AF.
AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=![]() AF.
AF.


科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成,根据两队每天的工程费用和每天完成的工程量可知,若由两队合做6天可以完成,共需工程费用385200元;若单独完成,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元。
(1)求甲、乙独做各需多少天?
(2)若从节省资金的角度,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
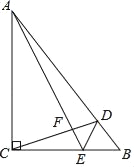
【题目】如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与AE交于点F,若∠AEC=∠DEB,CE=![]() ,则CF=______.
,则CF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算:观察下列式:
1⊙3=1×4+3=7 3⊙(﹣1)=3×4﹣1=11 5⊙4=5×4+4=24 4⊙(﹣3)=4×4﹣3=13
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填入“=”或“≠” )
(3)若a⊙(﹣2b)=3,请计算 (a﹣b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
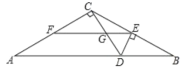
【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距高是![]() ;③AF=CF;④△ABF的面积为
;③AF=CF;④△ABF的面积为![]() 其中一定成立的有( )个.
其中一定成立的有( )个.
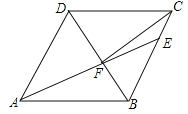
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度(a>150),那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果小张家八月份用电241度,那么这个月应交电费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com