
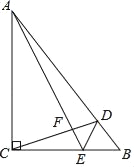
【题目】如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与AE交于点F,若∠AEC=∠DEB,CE=![]() ,则CF=______.
,则CF=______.
【答案】5
【解析】试题解析延长CE至G,使EC=EG,延长ED至H,使EH=AE,过D作DT∥BC,交AE于T,连接GH、AH,
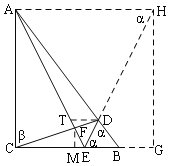
设∠AEC=α,则∠DEB=α,
∵∠AEC=∠DEB=α,
∴△AEC≌△DEB,
∴AC=GH,∠ACE=∠EGH=90°,
∴AC∥GH,
∴四边形ACGH是矩形,
∴AH∥CG,
∴∠AHE=∠HEG=α,
∵AC=AD,
∴∠ACD=∠ADC,
设∠ACD=∠ADC=β,
∵∠CDE=45°,
∴β+45°+∠BDE=180°,
∴β=135°-∠BDE①,
∵△ACD是等腰三角形,
∴∠CAD=180°-2β,
∵△ACB是直角三角形,
∴∠ABC=90°-∠CAD=90°-(180°-2β)=2β-90°,
在△BDE中,由内角和得:α+∠BDE+∠ABC=180°,
α+∠BDE+2β-90°=180°②,
把①代入②得:α+∠BDE+2(135°-∠BDE)-90°=180°,
∠BDE=α,
∴∠ADH=∠BDE=α,
∴AD=AH=AC,
∴四边形ACGH是正方形,
∴AH=AC=2CE=![]() ,
,
∴AD=AC=![]() ,
,
∵∠BED=∠BDE=α,
∴BE=BD,
设BE=x,则BD=x,
在Rt△ACB中,由勾股定理得:AC2+BC2=AB2,
∴(![]() )2+(
)2+(![]() +x)2=(
+x)2=(![]() +x)2,
+x)2,
解得:x=![]() ,
,
∴BE=BD=![]() ,
,
∴CE=2BE=2BD,
∴AD=4BD,
∴![]() ,
,
∵DT∥BC,
∴△ADT∽△ABE,
∴![]() ,
,
∵CE=2BE,
∴![]() ,
,
∵DT∥CE,
∴![]() ,
,
在Rt△ACE中,由勾股定理得:AE=![]()
∴ET=![]() AE=
AE=![]() ×
×![]() =
=![]() ,
,
∴EF=![]() ET=
ET=![]() ×
×![]() =
=![]() ,
,
过F作FM⊥BC于M,
tanα=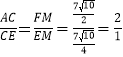 ,
,
设EM=y,则FM=2y,EF=![]() y,
y,
∴![]() y=
y=![]() ,
,
y=![]() ,
,
∴FM=2y=![]() ,EM=y=
,EM=y=![]() ,
,
∴CM=CE-EM=![]() -
-![]() =
=![]() ,
,
在Rt△CFM中,由勾股定理得:CF=![]() =5;
=5;
故答案为:5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
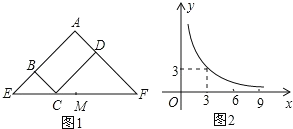
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xoy中,点P的坐标为(m+1,m-1).
(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
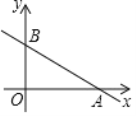
(2)如图,一次函数y= -![]() x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
(3)若点P在直线AB上,已知点R(![]() ,
,![]() ),S(
),S(![]() ,
,![]() )在直线y=kx+b上,b>2,
)在直线y=kx+b上,b>2,![]() +
+![]() =mb,
=mb, ![]() +
+![]() =kb+4若
=kb+4若![]() >
>![]() ,判断
,判断![]() 与
与![]() 的大小关系
的大小关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数![]() .按要求完成下列各题.
.按要求完成下列各题.
(1)请把题中各数填入相应的集合中:
①整数集合:{ …}
②负数集合:{ …}
(2)把题中各数用数轴上的点表示出来,并用“<“连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
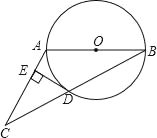
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=120°,⊙O的半径等于5,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
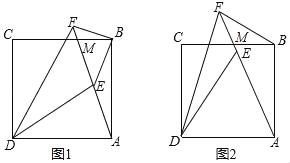
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2B. x2-62=(10-x)2
C. x2+62=(10-x)2D. x2+6=(10-x)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com