
【题目】(10分)如图,在平面直角坐标系中,反比例函数![]() 的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
(1)直接写出A、B、D三点的坐标;
(2)若将矩形只向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,求反比例函数的解析式和此时直线AC的解析式y=mx+n.并直接写出满足![]() 的x取值范围.
的x取值范围.

【答案】(1)A(﹣6,6),B(﹣6,4),D(﹣2,6);(2)![]() .
.
【解析】试题分析:(1)首先根据矩形的性质可知:点A、B的横坐标相同,B、C的纵坐标相同,A、D的纵坐标相同,C、D的横坐标相同,据此很容易写出点B、C、D的坐标;
(2)根据题意可知:平移后的矩形中B、D两点在y=kx的图象上;
设平移距离为a,则可以表示出点B′,点D′的坐标,将点B′、D′的坐标代入函数解析式,即可求出a的值,,进而得到A′、B′、C′、D′的坐标;将B′的坐标代入y=kx中得到反比例函数的解析式,将A′、C′代入直线中得到直线的解析式,据此相信你能解答本题了.
解:(1)A(﹣6,6),B(﹣6,4),D(﹣2,6);
(2)如图,矩形ABCD向下平移后得到矩形,
设平移距离为a,则B′(﹣6,4﹣a),D′(﹣2,6﹣a)∵点B′,点D′在y=![]() 的图象上,
的图象上,
∴﹣6(4﹣a)=﹣2(6﹣a),
解得a=3,
∴点A′(﹣6,3),B′(﹣6,1),C′(﹣2,1),D′(﹣2,3),
将点B′(﹣6,1)代入y=![]() 得:k=﹣6,
得:k=﹣6,
∴反比例函数的解析式为y=﹣![]() .
.
将A′(﹣6,3),C′(﹣2,1)点代入y=mx+n中得:![]() ,
,
解得:![]() ,
,
所以它的解析式为:![]()
满足![]() 的x取值范围即是
的x取值范围即是![]() 的取值范围,即:
的取值范围,即:![]() .
.



科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出BC边上的高线AE;
(3)利用网格点和三角板画图或计算:△A′B′C′的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读后填空:某家灯具厂为了比较甲、乙两种灯的使用寿命,各抽出8支做试验,结果如下(单位:小时).
甲:457,438,460,443,464,459,444,451;
乙:466,455,467,439,459,452,464,438.
试说明哪种灯的使用寿命长?哪种灯的质量比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的个数是 ( )
①若三条线段的比为1:1:![]() ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④有两个角相等的梯形是等腰梯形;⑤一条直线与矩形的一组对边相交,必分矩形为两个直角梯形。
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A.
B.
C.
D.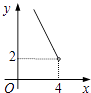
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一般的,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.﹣﹣苏科版《数学》九年级(下册)P21”参考上述教材中的话,判断方程x2﹣2x= ![]() ﹣2实数根的情况是( )
﹣2实数根的情况是( )
A.有三个实数根
B.有两个实数根
C.有一个实数根
D.无实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )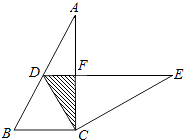
A.30,2
B.60,2
C.60, ![]()
D.60, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com