
【题目】如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )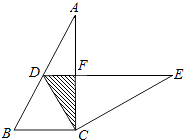
A.30,2
B.60,2
C.60, ![]()
D.60, ![]()
【答案】C
【解析】解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
∴∠B=60°,AC=BC×cot∠A=2× ![]() =2
=2 ![]() ,AB=2BC=4,
,AB=2BC=4,
∵△EDC是△ABC旋转而成,
∴BC=CD=BD= ![]() AB=2,
AB=2,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=60°,
∴∠DCF=30°,∠DFC=90°,即DE⊥AC,
∴DE∥BC,
∵BD= ![]() AB=2,
AB=2,
∴DF是△ABC的中位线,
∴DF= ![]() BC=
BC= ![]() ×2=1,CF=
×2=1,CF= ![]() AC=
AC= ![]() ×2
×2 ![]() =
= ![]() ,
,
∴S阴影= ![]() DF×CF=
DF×CF= ![]() ×
× ![]() =
= ![]() .
.
故答案为:C.
先根据已知条件求出AC的长及∠B的度数,再根据图形旋转的性质及等边三角形的判定定理判断出△BCD的形状,进而得出∠DCF的度数,由直角三角形的性质可判断出DF是△ABC的中位线,由三角形的面积公式即可得出结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,反比例函数![]() 的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
的图象和矩形ABCD在第二象限,AD平行于x轴,且AB=2,AD=4,点C的坐标为(﹣2,4).
(1)直接写出A、B、D三点的坐标;
(2)若将矩形只向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,求反比例函数的解析式和此时直线AC的解析式y=mx+n.并直接写出满足![]() 的x取值范围.
的x取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,
求证:∠3=∠B

证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥______( )
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等,两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行,同位角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某市中学生的幸福指数进行调查,从中抽取部分学生的调查表问卷进行统计,并绘制出不完整的统计表和条形统计图。
等级 | 频数 | 频率 |
★ | 60 | |
★★ | 80 | |
★★★ | 0.16 | |
★★★★ | 0.30 | |
★★★★★ |

(1)直接补全统计表;
(2)补全条形统计图(不要求写出计算过程);
(3)抽查的学生约占全市中学生的5%,估计全市约有多少名学生的幸福指数能达到五★级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=45°.以AB为直径的⊙O与BC相切于B,交AC于点D,CO的延长线交⊙O于点E,过点作弦EF⊥AB,垂足为点G.
(1)求证:①EF∥CB,②AD=CD;
(2)若AB=10,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:(1)两直线平行,内错角相等;(2)如果m是无理数,那么m是无限小数;(3)64的立方根是8;(4)同旁内角相等,两直线平行;(5)如果a是实数,那么![]() 是无理数.(6)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(7)直线外一点到这条直线的垂线段,叫做该点到直线的距离;(8)过一点作已知直线的平行线,有且只有一条.其中是真命题的有 ( )
是无理数.(6)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(7)直线外一点到这条直线的垂线段,叫做该点到直线的距离;(8)过一点作已知直线的平行线,有且只有一条.其中是真命题的有 ( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线CB//OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
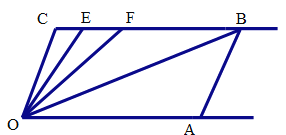
(1)求∠EOB的度数.(直接写出结果,无需解答过程)
∠EOB=__________°
(2)若在OC右侧左右平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,请找出变化规律;若不变,请求出这个比值.
(3)在OC右侧左右平行移动AB的过程中,是否存在使∠OEC=∠OBA的情况?若存在,请直接写出∠OEC度数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com