
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() .
.
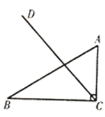
(1)尺规作图:作线段![]() 的垂直平分线
的垂直平分线![]() ;(要求:保留作图痕迹,不写作法)
;(要求:保留作图痕迹,不写作法)
(2)记直线![]() 与
与![]() ,
,![]() 的交点分别是点
的交点分别是点![]() ,
,![]() ,连接
,连接![]() 求证:
求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)利用尺规作出线段AB的垂直平分线l即可.
(2)想办法证明∠ECF=∠EFC=15°,根据等角对等边,EF=EC即可解决问题.
解:(1)如下图所示,直线l为线段AB的垂直平分线,
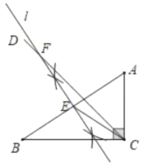
(2)∵∠ACB=90°,∠B=30°,
∴AC=![]() AB,∠A=60°.
AB,∠A=60°.
∵EF是AB的垂直平分线,
∴AE=![]() AB,∠AEF=90°,
AB,∠AEF=90°,
∴AE=AC,
∴△AEC是等边三角形,
∴∠AEC=∠ACE=60°,
∴∠FEC=∠AEF+∠AEC=150°.
∵CD平分∠ACB,
∴∠ACF=![]() ∠ACB=45°,
∠ACB=45°,
∴∠ECF=∠ECA﹣∠FCA=15°,
∴∠EFC=180°﹣∠FEC﹣∠ECF=15°=∠ECF,
∴EF=EC.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
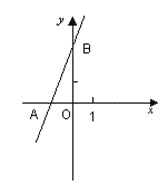
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.
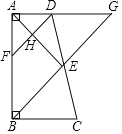
(1)求证:DG=BC;
(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.
(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
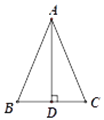
A.①②B.①②③C.①②③④D.①②③④⑤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).

解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
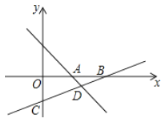
![]() 求直线
求直线![]() 的函数关系式;
的函数关系式;
![]() 点
点![]() 是
是![]() 上的一点,若
上的一点,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,是否存在
,是否存在![]() 的值使得
的值使得![]() 最小?若存在,请求出点
最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
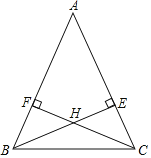
【题目】如图,AB=AC,BE与CF是△ABC的高线,且BE与CF相交于点H.
(1)求证:HB=HC;
(2)不添加辅助线,直接写出图中所有的全等三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com