
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
【答案】(1)证明见解析(2)4
【解析】(1)证明:∵将△BCE绕点C顺时针旋转到△DCF的位置,∴△BCE≌△DCF。∴∠FDC=∠EBC。
∵BE平分∠DBC,∴∠DBE=∠EBC。∴∠FDC=∠EBE。
又∵∠DGE=∠DGE,∴△BDG∽△DEG。
(2)解:∵△BCE≌△DCF,∴∠F=∠BEC,∠EBC=∠FDC。
∵四边形ABCD是正方形,∴∠DCB=90°,∠DBC=∠BDC=45°。
∵BE平分∠DBC,∴∠DBE=∠EBC=22.5°=∠FDC。
∴∠BDF=45°+22.5°=67.5°,∠F=90°﹣22.5°=67.5°=∠BDF。∴BD=BF,
∵△BCE≌△DCF,∴∠F=∠BEC=67.5°=∠DEG。
∴∠DGB=180°﹣22.5°﹣67.5°=90°,即BG⊥DF。
∵BD=BF,∴DF=2DG。
∵△BDG∽△DEG,BG×EG=4,∴![]() 。 ∴BG×EG=DG×DG=4。∴DG=2
。 ∴BG×EG=DG×DG=4。∴DG=2
∴BE=DF=2DG=4。
(1)根据旋转性质求出∠EDG=∠EBC=∠DBE,根据相似三角形的判定推出即可。
(2)先求出BD=BF,BG⊥DF,求出BE=DF=2DG,根据相似求出DG的长,即可求出答案


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
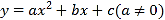
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)请求出抛物线的解析式;
(2)当0<x<4时,请直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在矩形ABCD中,AB=8,AD=3,点E是CD的中点,连接AE,将△ADE沿直线AE折叠,使点D落在点F处,则线段CF的长度是______.
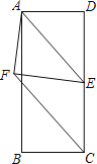
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有两个相等的实数根;④方程a(x﹣1)2+b(x﹣1)+c=0的两根是x1=﹣2,x2=2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到D需飞行15分钟.若无人机的配送路线是B→C→D→B请求出配送途中飞行所需时间.
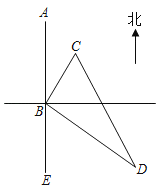
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=3,E在AC上且AE=![]() AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
AC,D是直线BC上一动点,线段ED绕点E逆时针旋转900,得到线段EF,当点D运动时,则线段AF的最小值是_______
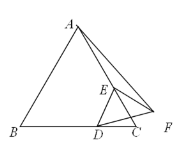
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com