
【题目】如图,⊙M交x轴于A(﹣1,0),B(3,0)两点.交y轴于C(0,3),D(0,1)两点.
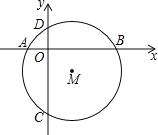
(1)求点M的坐标;
(2)求弧BD的长.
【答案】(1)M(1,﹣1);(2)![]() π.
π.
【解析】
试题分析:(1)过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,由垂径定理得出EB=![]() AB=2,得出OE=1,同理可得OF=1,证四边形OEMF为正方形,得出EM=EF=1,即可得出结果;
AB=2,得出OE=1,同理可得OF=1,证四边形OEMF为正方形,得出EM=EF=1,即可得出结果;
(2)连接MD,BC,由勾股定理可得BM=![]() ,证出∠BCO=45°,得出∠BMD=90°,由弧长公式即可得出结果.
,证出∠BCO=45°,得出∠BMD=90°,由弧长公式即可得出结果.
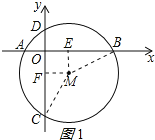
解:(1)如图1所示,过M点作ME⊥AB于E,MF⊥CD于F,连接MB,MC,
则EB=![]() AB=2,四边形OENF是矩形,
AB=2,四边形OENF是矩形,
∴OE=1,
同理可得OF=1,
∴OEOF,
∴四边形OEMF为正方形,
∴EM=EF=1,
∴M(1,﹣1);
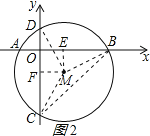
(2)连接MD,BC,如图2所示:
由勾股定理可得BM=![]() ,
,
∵∠BOC=90°,OB=OC,
∴∠BCO=45°,
∴∠BMD=90°,
∴弧BD的长=![]() =
=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】A、B坐标分别为A(1,0)、B(0,2),若将线段AB平移到A1B1,A与A1对应,A1、B1的坐标分别为A1(2,a),B1((b,3),则a+b= ___________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
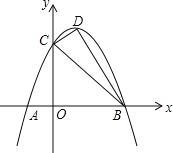
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
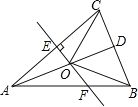
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm
C. 5cm,5cm,11cm D. 13cm,12cm,20cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com