
【题目】如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
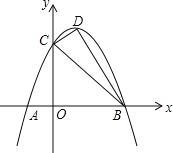
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3.(2)E(2,3).(3)存在,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.
【解析】
试题分析:(1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(﹣1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而可求得a=﹣1,b=2;
(2)过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点,由△BCD与△BCE是同底等高的三角形可知S△BCD=S△BCE,设直线DE的解析式为y=﹣x+b,将点D的坐标代入可求得直线DE的解析式,然后与抛物线的解析式联立可求得点E的坐标;
(3)由两点间的而距离公式可知:BC=3![]() ,CD=
,CD=![]() ,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
解:(1)∵将x=0代入得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1.
∴A(﹣1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(﹣1,0),B(3,0)代入y=ax2+bx+3得:![]() ,
,
解得:![]() .
.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵将x=1代入抛物线的解析式得:y=﹣1+2+3=4,
∴D(1,4).
如图1,过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点.
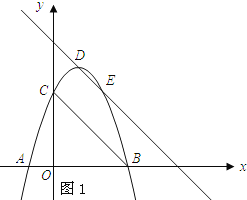
设直线DE的解析式为y=﹣x+b,
将点D的坐标代入得:﹣1+b=4,解得:b=5,则直线DE的解析式为y=﹣x+5.
将y=﹣x+5与y=﹣x2+2x+3联立得:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴E(2,3).
(3)存在.
由两点间的而距离公式可知:BC=![]() 3
3![]() ,CD=
,CD=![]() =
=![]() .
.
设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x.
①如图2所示:

∵当△BMN∽△DBC时,![]() ,
,
∴![]() .
.
解得:x1=2,x2=3(舍去).
∵当x=2时,y=3,
∴M(2,3).
②如图3所示:
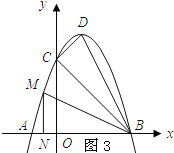
∵当△BMN∽△BDC时,![]() ,
,
∴![]() .
.
解得:x1=﹣![]() ,x2=3(舍去).
,x2=3(舍去).
当x=﹣![]() 时,y=
时,y=![]() ,
,
∴M(﹣![]() ,
,![]() )
)
综上,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
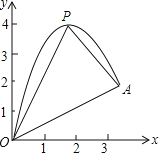
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太行山又名五行山、王母山、女娲山,是中国东部地区的重要山脉和地理分界线,绵延400余公里,400公里可以用科学记数法表示为( ).
A.4×104米 B.4×105米 C.0.4×106米 D.4×106米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,-1),则点B′的坐标为( )
A. (4,2) B. (5,2) C. (6,2) D. (5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )

A.小于0.64m3 B.大于0.64m3 C.不小于0.64m3 D.不大于0.64m3
查看答案和解析>>
科目:初中数学 来源: 题型:
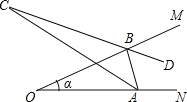
【题目】如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com