
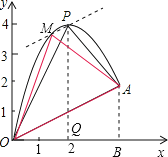
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
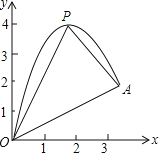
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
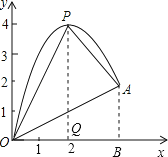
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
【答案】(1)(2,4);(2)(![]() ,
,![]() );(3)
);(3)![]() ;(4)点M的坐标为(
;(4)点M的坐标为(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;
(2)联立两解析式,可求出交点A的坐标;
(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=![]() x+b,将P(2,4)代入,求出直线PM的解析式为y=
x+b,将P(2,4)代入,求出直线PM的解析式为y=![]() x+3.再与抛物线的解析式联立,得到方程组
x+3.再与抛物线的解析式联立,得到方程组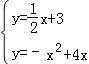 ,解方程组即可求出点M的坐标.
,解方程组即可求出点M的坐标.
解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得: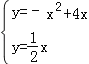 ,
,
解得:![]() ,或
,或![]() .
.
故可得点A的坐标为(![]() ,
,![]() );
);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=![]() x+b,
x+b,
∵P的坐标为(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直线PM的解析式为y=![]() x+3.
x+3.
由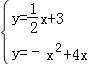 ,解得
,解得![]() ,
,![]() ,
,
∴点M的坐标为(![]() ,
,![]() ).
).


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有黄色、白色乒乓球共40个,除颜色外其他完全相同.小明从这个袋子中随机摸出一球,放回.通过多次摸球实验后发现,摸到黄色球的概率稳定在15%附近,则袋中黄色球可能有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电脑病毒传播快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.若每轮感染中平均一台电脑会感染x台电脑,则下面所列方程中正确的是( )
A.x(x+1)=81 B.1+x+x2=81
C.(1+x)2=81 D.1+(1+x)2=81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=![]() (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
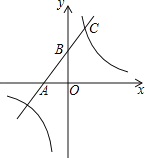
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
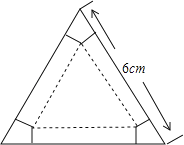
【题目】如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.![]() cm2 B.
cm2 B.![]()
![]() cm2 C.
cm2 C.![]()
![]() cm2 D.
cm2 D.![]()
![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
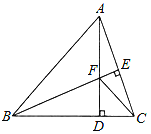
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
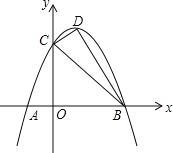
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com