
【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=![]() (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
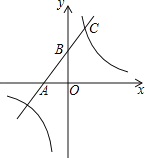
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
【答案】(1)A(﹣2,0),y=x+2.(2)(2,4),y=![]() .
.
【解析】
试题分析:(1)根据OA=OB和点B的坐标易得点A坐标,再将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,;
(2)由B是线段AC的中点,可得C点坐标,将C点坐标代入y=![]() (k≠0)可确定反比例函数的解析式.
(k≠0)可确定反比例函数的解析式.
解:(1)∵OA=OB,点B的坐标为(0,2),
∴点A(﹣2,0),
点A、B在一次函数y=kx+b(k≠0)的图象上,
∴![]() ,
,
解得k=1,b=2,
∴一次函数的解析式为y=x+2.
(2)∵B是线段AC的中点,
∴点C的坐标为(2,4),
又∵点C在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=8;
∴反比例函数的解析式为y=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
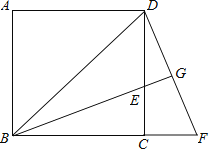
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
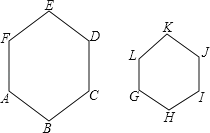
A.∠E=2∠K
B.BC=2HI
C.六边形ABCDEF的周长=六边形GHIJKL的周长
D.S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
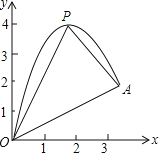
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )

A.小于0.64m3 B.大于0.64m3 C.不小于0.64m3 D.不大于0.64m3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com