
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
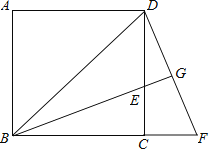
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
【答案】(1)见解析;(2)4
【解析】
试题分析:(1)根据旋转性质求出∠EDG=∠EBC=∠DBE,根据相似三角形的判定推出即可;
(2)先求出BD=BF,BG⊥DF,求出BE=DF=2DG,根据相似求出DG的长,即可求出答案.
(1)证明:∵将△BCE绕点C顺时针旋转到△DCF的位置,
∴△BCE≌△DCF,
∴∠FDC=∠EBC,
∵BE平分∠DBC,
∴∠DBE=∠EBC,
∴∠FDC=∠EBD,
∵∠DGE=∠DGE,
∴△BDG∽△DEG.
(2)解:∵△BCE≌△DCF,
∴∠F=∠BEC,∠EBC=∠FDC,
∵四边形ABCD是正方形,
∴∠DCB=90°,∠DBC=∠BDC=45°,
∵BE平分∠DBC,
∴∠DBE=∠EBC=22.5°=∠FDC,
∴∠BEC=67.5°=∠DEG,
∴∠DGE=180°﹣22.5°﹣67.5°=90°,
即BG⊥DF,
∵∠BDF=45°+22.5°=67.5°,∠F=90°﹣22.5°=67.5°,
∴∠BDF=∠F,
∴BD=BF,
∴DF=2DG,
∵△BDG∽△DEG,BG×EG=4,
∴![]() =
=![]() ,
,
∴BG×EG=DG×DG=4,
∴DG2=4,
∴DG=2,
∴BE=DF=2DG=4.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】下列语句中,真命题有( )个
①在同一平面内,过一点有且只有一条直线与已知直线平行;
②相等的角是对顶角;
③若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角;
④平方根和立方根相等的数是0;
⑤平移变换中,各组对应点连成的线段平行且相等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
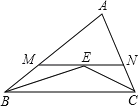
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电脑病毒传播快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.若每轮感染中平均一台电脑会感染x台电脑,则下面所列方程中正确的是( )
A.x(x+1)=81 B.1+x+x2=81
C.(1+x)2=81 D.1+(1+x)2=81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定△ABC是等腰三角形的是( )
A.a=3,b=3,c=4 B.a︰b︰c=2︰3︰4
C.∠B=50°,∠C=80° D.∠A︰∠B︰∠C=1︰1︰2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=![]() (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
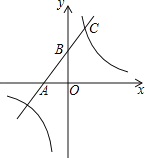
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B坐标分别为A(1,0)、B(0,2),若将线段AB平移到A1B1,A与A1对应,A1、B1的坐标分别为A1(2,a),B1((b,3),则a+b= ___________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com