
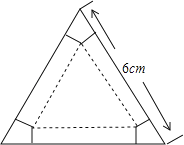
【题目】如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.![]() cm2 B.
cm2 B.![]()
![]() cm2 C.
cm2 C.![]()
![]() cm2 D.
cm2 D.![]()
![]() cm2
cm2
【答案】C
【解析】
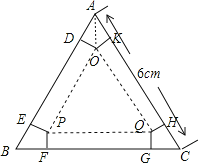
试题分析:如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD=![]() x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
![]() ,
,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=![]() x,
x,
∴DE=6﹣2![]() x,
x,
∴纸盒侧面积=3x(6﹣2![]() x)=﹣6
x)=﹣6![]() x2+18x,
x2+18x,
=﹣6![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,纸盒侧面积最大为
时,纸盒侧面积最大为![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点A在m上,点B、C、D在n上,且AB=4cm,AC=5cm,AD=6cm,则m与n之间的距离( )
A. 等于5cm B. 等于6cm C. 等于4cm D. 小于或等于4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
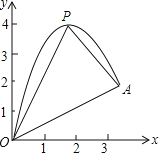
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
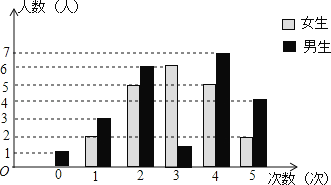
(1)该班级女生人数是 ;女生收看“两会”新闻次数的众数是 ;中位数是 .
(2)求女生收看次数的平均数.
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明计算出女生收看“两会”新闻次数的方差为![]() ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
(4)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”,如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
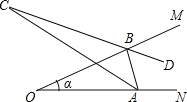
【题目】如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com