
【题目】如图,已知△ABC,AB、AC的垂直平分线的交点D恰好落在BC边上
(1)判断△ABC的形状
(2)若点A在线段DC的垂直平分线上,求![]() 的值
的值

科目:初中数学 来源: 题型:
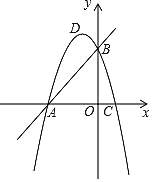
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
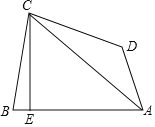
【题目】如图,在四边形ABCD中,AC是四边形的对角线,∠CAD=30°,过点C作CE⊥AB于点E,∠B=2∠BAC,∠ADC﹣∠BAC=90°,若AB=20,CD=16,则BE的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
科目:初中数学 来源: 题型:
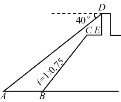
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为__米.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
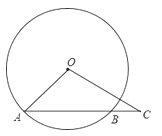
【题目】如图,某新建公园有一个圆形人工湖,湖中心O处有一座喷泉,小明为测量湖的半径,在湖边选择A、B两个点,在A处测得∠OAB=45°,在AB延长线上的C处测得∠OCA=30°,已知BC=50米,求人工湖的半径.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com