
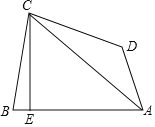
【题目】如图,在四边形ABCD中,AC是四边形的对角线,∠CAD=30°,过点C作CE⊥AB于点E,∠B=2∠BAC,∠ADC﹣∠BAC=90°,若AB=20,CD=16,则BE的长为____.
【答案】2.
【解析】
在EA上截取EF=EB,连接CF,作FM⊥AC于M,作CN⊥AD于N,由线段垂直平分线的性质得出CB=CF,由等腰三角形的性质得出∠CFB=∠B=2∠BAC,证出∠FCA=∠BAC,得出AF=CF,由等腰三角形的性质得出CM=AM=![]() AC,由直角三角形的性质得出CN=
AC,由直角三角形的性质得出CN=![]() AC,得出AM=CN,证出∠BAC=∠DCN,证明△AFM≌△CDN(ASA),得出AF=CD=16,进而得出答案.
AC,得出AM=CN,证出∠BAC=∠DCN,证明△AFM≌△CDN(ASA),得出AF=CD=16,进而得出答案.
在EA上截取EF=EB,连接CF,作FM⊥AC于M,作CN⊥AD于N,如图所示:
∵CE⊥AB,
∴CB=CF,
∴∠CFB=∠B=2∠BAC.
∵∠CFB=∠FCA+∠BAC,
∴∠FCA=∠BAC,
∴AF=CF.
∵FM⊥AC,
∴CM=AM=![]() AC.
AC.
∵CN⊥AD,∠CAD=30![]() ,
,
∴CN=![]() AC,
AC,
∴AM=CN.
∵∠ADC﹣∠BAC=90![]() ,
,
∴∠ADC=90![]() +∠BAC.
+∠BAC.
∵∠ADC=∠N+∠DCN=90![]() +∠DCN,
+∠DCN,
∴∠BAC=∠DCN,
在△AFM和△CDN中, ,
,
∴△AFM≌△CDN(ASA),
∴AF=CD=16,
∴BF=AB﹣AF=20﹣16=4,
∴BE=![]() BF=2.
BF=2.
故答案为:2.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,经过点(-1,0),有下列结论:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正确的结论有( )
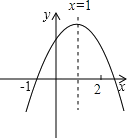
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AC的表达式为y=![]() x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
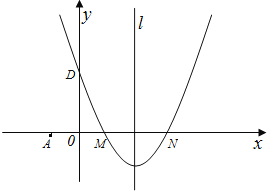
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
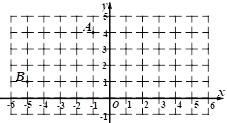
【题目】点A(1,4)和点B(5,1)在平面直角坐标系中的位置如图所示:
(1)点A1、B1分别为点A、B关于y轴的对称点,请画出四边形AA1B1B,并写出A1、B1的坐标;
(2)在(1)的条件下,画一条过四边形AA1B1B的一个顶点的线段,将四边形AA1B1B分成两个图形,并且使分得的图形中的一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α cos α;
若α<45°,则sin α cos α;
若α>45°,则sin α cos α.
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
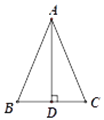
A.①②B.①②③C.①②③④D.①②③④⑤.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com